
分析 (Ⅰ)a=0时,可求出f(x),进而得出$f′(x)=\frac{2x-1}{{x}^{2}}$,根据导数符号便可得出f(x)的极小值点,并求得该极小值,并判断无极大值;
(Ⅱ)求导数得到$f′(x)=\frac{2a(x+\frac{1}{a})(x-\frac{1}{2})}{{x}^{2}}$,根据a的范围,及x∈[1,2]便可判断f′(x)<0在[1,2]上成立,即f(x)在区间[1,2]上单调递减,从而|f(x1)-f(x2)|在x1,x2∈[1,2]上的最大值为f(1)-f(2)=$(a-2)ln2+\frac{1}{2}-2a$,根据条件即可整理得到$ma<\frac{1}{2}$,从而得到$m>\frac{1}{2a}$,可求出$\frac{1}{2a}$的范围,从而求出m的取值范围.
解答 解:(Ⅰ)a=0时,$f(x)=2lnx+\frac{1}{x}$,$f'(x)=\frac{2}{x}-\frac{1}{x^2}=\frac{2x-1}{x^2}$;
令f'(x)=0,$x=\frac{1}{2}$;
∴$0<x<\frac{1}{2}$时,f'(x)<0,当$x>\frac{1}{2}$时,f'(x)>0;
∴$x=\frac{1}{2}$时,f(x)取得极小值2-2ln2,无极大值;
(Ⅱ)$f'(x)=\frac{2-a}{x}-\frac{1}{x^2}+2a=\frac{(ax+1)(2x-1)}{x^2}=\frac{{2a(x+\frac{1}{a})(x-\frac{1}{2})}}{x^2}$;
∵a∈(-3,-2),$-\frac{1}{2}<\frac{1}{a}<-\frac{1}{3}$;
∴x∈[1,2]时,f'(x)<0,f(x)单调递减;
∴$|f({x_1})-f({x_2}){|_{max}}=f(1)-f(2)=(a-2)ln2+\frac{1}{2}-2a$;
因为存在x1,x2∈[1,2],使不等式|f(x1)-f(x2)|>(m-2+ln2)a-2ln2成立;
∴$(a-2)ln2+\frac{1}{2}-2a>(m-2+ln2)a-2ln2$
化简得$ma<\frac{1}{2}$,又-3<a<-2
∴$m>\frac{1}{2a}$,$\frac{1}{2a}∈(-\frac{1}{4},-\frac{1}{6})$;
∴$m≥-\frac{1}{6}$;
∴m的取值范围为$[-\frac{1}{6},+∞)$.
点评 考查基本初等函数的求导公式,函数极值的定义及求法,根据导数符号判断函数单调性的方法,以及单调性定义的运用,恒成立问题的解决方法,不等式的性质.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
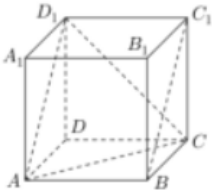 如图,正方体ABCD-A1B1C1D1,则下列四个命题:
如图,正方体ABCD-A1B1C1D1,则下列四个命题:| A. | ①③ | B. | ①③④ | C. | ①②④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | 8 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
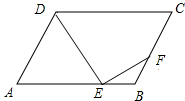 如图,在平行四边形ABCD中,AB=4,AD=2,∠BAD=60°,E,F分别为AB,BC上的点,且AE=2EB,CF=2FB.
如图,在平行四边形ABCD中,AB=4,AD=2,∠BAD=60°,E,F分别为AB,BC上的点,且AE=2EB,CF=2FB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{4}{5}$ | C. | $\frac{5}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com