Question

13．在三棱柱ABC-A₁B₁C₁中，AA₁⊥BC，A₁B⊥AC．D，E分别是BB₁，A₁C₁的中点．
（Ⅰ）求证：DE∥平面A₁BC；
（Ⅱ）若AB⊥BC，求证：A₁B⊥面ABC；
（Ⅲ）在（Ⅱ）的条件下，AB=BC=1，$B{B_1}=\sqrt{2}$，求三棱锥A₁-BCC₁的体积．

Answer 1

分析 （Ⅰ）取A₁C中点F，连接BF，EF，可证EF∥CC₁，且$EF=\frac{1}{2}C{C_1}$，又由CC₁∥BB₁，D是BB₁的中点，可证EF∥DB，且EF=DB，从而证明DE∥BF，即可证明DE∥平面A₁BC．
（Ⅱ）由已知可证BC⊥平面ABB₁A₁，既有BC⊥A₁B．又A₁B⊥AC，AC∩BC=C，即可证明A₁B⊥面ABC．
（Ⅲ）由（Ⅱ）的结论得A₁B⊥AB，可证AB⊥平面A₁BC，A₁B₁⊥平面A₁BC，B₁C₁∥平面A₁BC，由已知可求A₁B=1，从而可求三棱锥A₁-BCC₁的体积．

解答 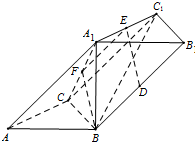解：（Ⅰ）取A₁C中点F，连接BF，EF，
∵E是A₁C₁的中点，
∴EF∥CC₁，且$EF=\frac{1}{2}C{C_1}$，
又∵CC₁∥BB₁，D是BB₁的中点，
∴EF∥DB，且EF=DB，
∴四边形BDEF是平行四边形，
∴DE∥BF，而DE?平面A₁BC，BF?平面A₁BC，
∴DE∥平面A₁BC．…4分
（Ⅱ）∵AA₁⊥BC，AB⊥BC，而AB∩A₁B=B，
∴BC⊥平面ABB₁A₁，
∴BC⊥A₁B．
又∵A₁B⊥AC，AC∩BC=C，
∴A₁B⊥面ABC．…8分
（Ⅲ）由（Ⅱ）的结论得A₁B⊥AB，
∵AB⊥BC，∴AB⊥平面A₁BC；
∵A₁B₁∥AB，∴A₁B₁⊥平面A₁BC．
由B₁C₁∥BC可知，B₁C₁∥平面A₁BC；
∵AB=1=A₁B₁，$A{A_1}=B{B_1}=\sqrt{2}$，
∴A₁B=1，
∴三棱锥A₁-BCC₁的体积：${V_{{A_1}-BC{C_1}}}={V_{{C_1}-{A_1}BC}}={V_{{B_1}-{A_1}BC}}=\frac{1}{3}{S_{△{A_1}BC}}•{A_1}{B_1}=\frac{1}{3}•\frac{1}{2}•1=\frac{1}{6}$．…12分．

点评 本题考查线面平行、垂直关系的判定与性质等基础知识，考查空间想象能力，属于中等题．