
分析 (I)通过已知条件,利用递推关系可得bn+1-bn=1且b1=1,进而可得结论;
(II)(i)问题即为证明|sinnθ|≤n|sinθ|,利用数学归纳法、三角函数的和角公式及三角函数的有界性即可;(ii)通过cn=Sn-n+1+lnn,得cn+1-cn=$-\frac{1}{n+1}+ln\frac{n+1}{n}$,令$\frac{1}{n+1}$=x,且$0<x≤\frac{1}{3}$,通过求导可得f(x)=-x-ln(1-x)在$({0,\frac{1}{3}}]$单调递增,进而可得结论.
解答 (I)解:∵an+1=$\frac{1}{2-{a}_{n}}$,bn=$\frac{1}{1-{a}_{n}}$,
∴bn+1=$\frac{1}{1-{a}_{n+1}}$=$\frac{1}{1-\frac{1}{2-{a}_{n}}}$=$\frac{2-{a}_{n}}{1-{a}_{n}}$=1+$\frac{1}{1-{a}_{n}}$=1+bn,
所以bn+1-bn=1且b1=$\frac{1}{1-0}$=1,
故数列{bn}是以首项、公差均为1的等差数列,
所以bn=n;
(II)证明:
(i)由(I)知,bn=n,
要证|sin(bn•θ)|≤bn|sinθ|,只需证|sinnθ|≤n|sinθ|.
下面用数学归纳法证明:
①当n=1时,|sinθ|=|sinθ|,结论成立.
②假设当n=k(k≥1)时结论成立,即|sinkθ|≤k|sinθ|.
那么,当n=k+1时,
|sin(k+1)θ|=|sinkθcosθ+coskθsinθ|
≤|sinkθcosθ|+|coskθsinθ|
=|sinkθ||cosθ|+|coskθ||sinθ|
≤|sinkθ|+|sinθ|
≤k|sinθ|+|sinθ|
=(k+1)|sinθ|,即结论成立.
由①②可知,结论对一切正整数n都成立;
(ii)∵cn=Sn-n+1+lnn,
∴cn+1-cn=Sn+1-(n+1)+1+ln(n+1)-Sn+n-1-lnn
=${a_{n+1}}-1+ln\frac{n+1}{n}$
=$-\frac{1}{n+1}+ln\frac{n+1}{n}$,
令$\frac{1}{n+1}$=x,且$0<x≤\frac{1}{3}$,
记f(x)=-x-ln(1-x),
∵f′(x)=-1+$\frac{1}{1-x}$=$\frac{x}{1-x}$>0,
∴f(x)在$({0,\frac{1}{3}}]$单调递增,则f(x)>f(0)=0,
即cn+1-cn>0,cn+1>cn.
故数列{cn}是递增数列.
点评 本题考查数列的递推性质,考查等差数列的通项公式、数学归纳法,涉及到三角函数的和角公式、有界性,考查分析问题、解决问题及计算能力,对表达式的灵活变形是解决本题的关键,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-1,2) | C. | {-1,0,1} | D. | {-1,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+3y+5=0 | B. | 3x-y-5=0 | C. | 3x+y-1=0 | D. | x-3y-7=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在三棱柱ABC-A1B1C1中,AA1⊥BC,A1B⊥AC.D,E分别是BB1,A1C1的中点.
在三棱柱ABC-A1B1C1中,AA1⊥BC,A1B⊥AC.D,E分别是BB1,A1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
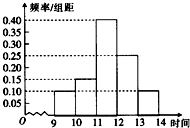 某商场在今年元霄节的促销活动中,对3月5日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为5万元,则11时至12时的销售额为( )
某商场在今年元霄节的促销活动中,对3月5日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为5万元,则11时至12时的销售额为( )| A. | 10万元 | B. | 15万元 | C. | 20万元 | D. | 25万元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com