
分析 (1)通过S4=3S2+2、a2n=2an计算即可;
(2)通过分离分母,并项相加即得结论.
解答 解:(1)设等差数列{an}的首项为a1,公差为d,
则由S4=3S2+2、a2n=2an,得$\left\{{\begin{array}{l}{4{a_1}+6d=3(2{a_1}+d)+2}\\{{a_1}+(2n-1)d=2[{a_1}+(n-1)d]}\end{array}}\right.$,
解得$\left\{{\begin{array}{l}{{a_1}=2}\\{d=2}\end{array}}\right.$,所以${a_n}=2n,n∈{N^*}$;
(2)因为${a_n}=2n,n∈{N^*}$,
所以${b_n}=\frac{2n+1}{{{{(n+1)}^2}4{n^2}}}=\frac{1}{4}[\frac{1}{n^2}-\frac{1}{{{{(n+1)}^2}}}]$,
则${T_n}=\frac{1}{4}[1-\frac{1}{2^2}+\frac{1}{2^2}-\frac{1}{3^2}+\frac{1}{3^2}-\frac{1}{4^2}+…+\frac{1}{n^2}-\frac{1}{{{{(n+1)}^2}}}]$=$\frac{1}{4}[1-\frac{1}{{{{(n+1)}^2}}}]$.
因为n≥1,n∈N*,所以$\frac{3}{16}≤{T_n}<\frac{1}{4}$.
点评 本题考查求数列的通项及前n项和,分离分母且并项相加是解决本题的关键,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{16\sqrt{6}}{3}$ | B. | 8 | C. | $\frac{5\sqrt{15}}{3}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$或$\frac{1}{16}$ | C. | $\frac{1}{16}$ | D. | $\frac{\sqrt{3}}{2}$或$\frac{1}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北邢台市高一上学期月考一数学试卷(解析版) 题型:解答题
已知函数
(1)求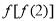 并判断函数
并判断函数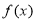 的奇偶性;
的奇偶性;
(2)若对任意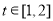 ,
,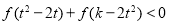 恒成立,求实数
恒成立,求实数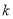 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com