
分析 n=1时,$\frac{{a}_{1}}{3}$=$\frac{1}{2}$,可得a1.n≥2时,$\sum_{i=1}^{n}$(-1)i+1$\frac{{a}_{i}}{{2}^{i}+1}$=$\frac{1}{{2}^{n}}$,$\sum_{i=1}^{n-1}$(-1)i$•\frac{{a}_{i}}{{2}^{i}+1}$=$\frac{1}{{2}^{n-1}}$,相减可得:(-1)n$\frac{{a}_{n}}{{2}^{n}+1}$=$\frac{1}{{2}^{n}}$,可得an.
解答 解:n=1时,$\frac{{a}_{1}}{3}$=$\frac{1}{2}$,∴a1=$\frac{3}{2}$.
n≥2时,$\sum_{i=1}^{n}$(-1)i+1$\frac{{a}_{i}}{{2}^{i}+1}$=$\frac{1}{{2}^{n}}$,$\sum_{i=1}^{n-1}$(-1)i$•\frac{{a}_{i}}{{2}^{i}+1}$=$\frac{1}{{2}^{n-1}}$,相减可得:(-1)n$\frac{{a}_{n}}{{2}^{n}+1}$=$\frac{1}{{2}^{n}}$,可得an=(-1)n$(1+\frac{1}{{2}^{n}})$.
∴an=$\left\{\begin{array}{l}{\frac{3}{2},n=1}\\{(-1)^{n}(\frac{1}{{2}^{n}}+1),n≥2}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{\frac{3}{2},n=1}\\{(-1)^{n}(\frac{1}{{2}^{n}}+1),n≥2}\end{array}\right.$.
点评 本题考查了等数列递推关系、数列通项公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP=2,AB=2$\sqrt{7}$,E为棱PD中点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP=2,AB=2$\sqrt{7}$,E为棱PD中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
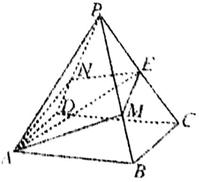 如图,在正四棱锥P-ABCD中,AB=2,PA=$\sqrt{6}$,E是棱PC上的点,过AE作平面分别与棱PB、PD交于M、N两点,且$\frac{PM}{PB}$=$\frac{PN}{PD}$=$\frac{2}{3}$.
如图,在正四棱锥P-ABCD中,AB=2,PA=$\sqrt{6}$,E是棱PC上的点,过AE作平面分别与棱PB、PD交于M、N两点,且$\frac{PM}{PB}$=$\frac{PN}{PD}$=$\frac{2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+$\sqrt{3}$y-2=0 | B. | x+$\sqrt{3}$y-4=0 | C. | $\sqrt{3}$x+y-2=0 | D. | x+$\sqrt{3}$y-6=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
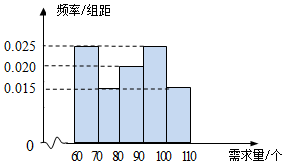 在某单位的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以x(单位:个,60≤x≤110)表示面包的需求量,T(单位:元)表示利润.
在某单位的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以x(单位:个,60≤x≤110)表示面包的需求量,T(单位:元)表示利润.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| A | 4 | 4 | 4.5 | 5 | 5.5 | 6 | 6 | |||
| B | 4.5 | 5 | 6 | 6.5 | 6.5 | 7 | 7 | 7.5 | ||
| C | 5 | 5 | 5.5 | 6 | 6 | 7 | 7 | 7.5 | 8 | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com