练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．$\frac{sin（-340°）sin70°}{co{s}^{2}155°-si{n}^{2}25°}$的值是$\frac{1}{2}$．

    分析 直接利用诱导公式及倍角公式化简求值．

    解答 解：$\frac{sin（-340°）sin70°}{co{s}^{2}155°-si{n}^{2}25°}$=$\frac{sin（-360°+20°）cos20°}{co{s}^{2}25°-si{n}^{2}25°}$
    =$\frac{sin20°cos20°}{cos50°}=\frac{2sin20°cos20°}{2cos50°}$=$\frac{sin40°}{2sin40°}=\frac{1}{2}$．
    故答案为：$\frac{1}{2}$．

    点评 本题考查三角函数的化简求值，考查了倍角公式及诱导公式的应用，是基础的计算题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．已知f（x）=2sin（$\frac{x}{2}$+$\frac{π}{6}$）
    （1）若向量$\overrightarrow{m}$=（$\sqrt{3}$cos$\frac{x}{4}$，cos$\frac{x}{4}$），$\overrightarrow{n}$=（-cos$\frac{x}{4}$，sin$\frac{x}{4}$），且$\overrightarrow{m}$∥$\overrightarrow{n}$，求f（x）的值；
    （2）在△ABC中，角A，B，C的对边分别是a，b，c，且满足（$\sqrt{2}$a-c）cosB=bcosC，求f（A）的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知数列{an}前n项和满足Sn-Sn-1=$\sqrt{{S}_{n}}$+$\sqrt{{S}_{n-1}}$  （n≥2），a1=1，则an=（　　）
    A．nB．2n-1C．n2D．2n2-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知函数f（x）=（$\frac{1}{3}$）x，a＞0，b＞0，a≠b，m=f（$\frac{a+b}{2}$），n=f（$\sqrt{ab}$），p=f（$\frac{2ab}{a+b}$），则m，n，p 的大小关系为（　　）
    A．m＜n＜pB．m＜p＜nC．p＜m＜nD．p＜n＜m

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．$\sqrt{si{n}^{2}480°}$等于（　　）
    A．±$\frac{\sqrt{3}}{2}$B．$\frac{\sqrt{3}}{2}$C．-$\frac{\sqrt{3}}{2}$D．$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

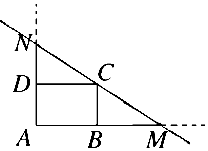    19．如图，已知矩形ABCD中，AB=6，AD=4，过点C的直线l与AB，AD的延长线分别交于点M，N．
    （1）若△AMN的面积不小于50，求线段DN的长度的取值范围；
    （2）在直线l绕点C旋转的过程中，△AMN的面积S是否存在最小值？若存在，求出这个最小值及相应的AM，AN的长度；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知三角形的三个顶点A（-5，0），B（3，-3），C（0，2），求AB边所在直线的方程及该边上高线所在直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知向量$\overrightarrow{a}$=（cosθ，sinθ），θ∈（0，π），$\overrightarrow{b}$=（1，$\sqrt{3}$），若$\overrightarrow{a}$与$\overrightarrow{b}$共线，则sin2θ=（　　）
    A．$\frac{1}{2}$B．$\frac{\sqrt{3}}{2}$C．-$\frac{1}{2}$D．-$\frac{\sqrt{3}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知定点A（12，0），M为曲线$\left\{{\begin{array}{l}{x=6+2cosθ}\\{y=2sinθ}\end{array}}$上的动点．
    （1）若点P满足条件$\overrightarrow{AP}=2\overrightarrow{AM}$，试求动点P的轨迹C的方程；
    （2）在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，若直线：ρcosθ+ρsinθ=a与曲线C相交于不同的E、F两点，O为坐标原点且$\overrightarrow{OE}•\overrightarrow{OF}$=12，求∠EOF的余弦值和实数a的值．

    查看答案和解析>>

    同步练习册答案