
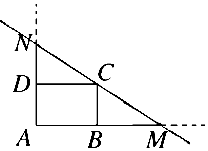
 如图,已知矩形ABCD中,AB=6,AD=4,过点C的直线l与AB,AD的延长线分别交于点M,N.
如图,已知矩形ABCD中,AB=6,AD=4,过点C的直线l与AB,AD的延长线分别交于点M,N.分析 (1)设DN=x(x>0),通过△NDC~△NAM,得到$\frac{x}{4+x}=\frac{6}{AM}$,然后求出三角形的面积的表达式,利用面积的范围求解即可.
(2)利用面积的表达式,利用基本不等式求解面积的最小值即可.
解答 解:(1)设DN=x(x>0),△AMN的面积为S,
∵△NDC~△NAM,∴$\frac{x}{4+x}=\frac{6}{AM}$,∴$AM=\frac{6(x+4)}{x}$,
∴$S=\frac{1}{2}AM•AN=\frac{1}{2}•\frac{6(x+4)}{x}•(x+4)=3•\frac{{{{(x+4)}^2}}}{x}$.
由$S=3•\frac{{{{(x+4)}^2}}}{x}≥50$,得$0<x≤\frac{8}{3}$或x≥6.
所以,线段DN的长度的取值范围$(0,\frac{8}{3}]∪[6,+∞)$.
(2)$S=3•\frac{{{{(x+4)}^2}}}{x}=3•(x+\frac{16}{x}+8)$
因为x>0,∴$S=3•(x+\frac{16}{x}+8)≥3(2\sqrt{x•\frac{16}{x}}+8)=48$,
当且仅当$x=\frac{16}{x}$,即x=4,等号成立,此时AM=12,
故存在M,N点,当AM=12,AN=8,△AMN的面积S有最小值48.
点评 本题考查函数的模型的选择与应用,二次函数的性质的应用,基本不等式求解表达式的最值,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | n | B. | 2n | C. | 3n | D. | 4n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤-$\frac{1}{2}$ | B. | -$\frac{1}{2}$≤a<0 | C. | 0<a≤$\frac{1}{2}$ | D. | a≥$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x=2,则x2=4”的逆命题为真命题 | |
| B. | 命题“p或q”为真,“非p”为假,则q可真可假 | |
| C. | 命题“若log2x2=2,则x=2”的否命题为:“若log2x2=2,则x≠2” | |
| D. | 命题“?x∈R使得2x<1”的否定是:“?x∈R均有2x>1” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com