
分析 根据条件便可由正弦定理分别得到$\frac{BD}{sin15°}$=$\frac{3}{sin∠BDA}$①$\frac{BE}{sin75°}$=$\frac{3}{sin∠AEB}$②$\frac{CE}{sin15°}$=$\frac{4}{sin∠AEB}$③$\frac{CD}{sin75°}$=$\frac{4}{sin∠BDA}$④,而sin∠BDA=sin∠ADC,sin∠BEA=sin∠AEC,从而$\frac{①}{④}•\frac{②}{③}$得:$\frac{BD•BE}{CD•CE}$的值.
解答 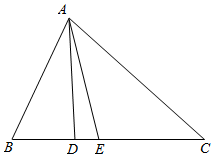 解:如图,由正弦定理得,$\frac{BD}{sin15°}$=$\frac{3}{sin∠BDA}$①
解:如图,由正弦定理得,$\frac{BD}{sin15°}$=$\frac{3}{sin∠BDA}$①
$\frac{BE}{sin75°}$=$\frac{3}{sin∠AEB}$②
$\frac{CE}{sin15°}$=$\frac{4}{sin∠AEB}$③
$\frac{CD}{sin75°}$=$\frac{4}{sin∠BDA}$④
∴$\frac{①}{④}•\frac{②}{③}$得:$\frac{BD•BE}{CD•CE}$=$\frac{9}{16}$.
故答案为$\frac{9}{16}$.
点评 考查正弦定理以及三角函数的诱导公式:sin(π-α)=sinα,考查学生分析解决问题的能力,正确运用正弦定理是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
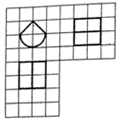 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中曲线部分是圆弧,则此几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中曲线部分是圆弧,则此几何体的表面积为( )| A. | 2+4$\sqrt{2}$+3π | B. | 2+4$\sqrt{2}$+5π | C. | 10+π | D. | 20+2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,将绘有函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$<φ<π)的部分图象的纸片沿x轴折成直二面角,若AB之间的空间距离为2$\sqrt{3}$,则f(-1)=( )
如图,将绘有函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$<φ<π)的部分图象的纸片沿x轴折成直二面角,若AB之间的空间距离为2$\sqrt{3}$,则f(-1)=( )| A. | -2 | B. | 2 | C. | -$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com