
分析 先根据定积分的计算得到$\frac{1}{a}$+$\frac{4}{b}$=1,由题知利用“1”的代换,以及基本不等式求解即可得到答案.
解答 解:∵${∫}_{0}^{\frac{π}{2}}$cosxdx=sinx|${\;}_{0}^{\frac{π}{2}}$=1,
∴$\frac{1}{a}$+$\frac{4}{b}$=1,
∵a,b均为正数,
∴a+b=(a+b)($\frac{1}{a}$+$\frac{4}{b}$)=5+$\frac{b}{a}$+$\frac{4a}{b}$≥5+2$\sqrt{\frac{b}{a}•\frac{4a}{b}}$=9.当且仅当a=3,b=6时取等号.
∴a+b>c恒成立的实数c的取值范围是c<9.
故答案为:(-∞,9).
点评 本题考查定积分的计算,基本不等式的应用,解题时要认真审题,仔细解答.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
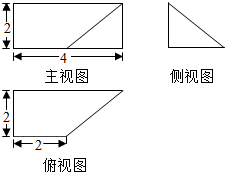
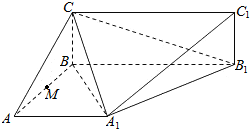
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
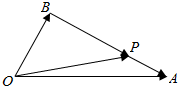 如图,在△OAB中,已知P为线段AB上一点,$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$.
如图,在△OAB中,已知P为线段AB上一点,$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com