
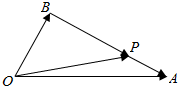
 如图,在△OAB中,已知P为线段AB上一点,$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$.
如图,在△OAB中,已知P为线段AB上一点,$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$.分析 (1)用$\overrightarrow{OA},\overrightarrow{OB}$表示出$\overrightarrow{OP}$,根据平面向量的基本定理得出x,y;
(2)用$\overrightarrow{OA},\overrightarrow{OB}$表示出$\overrightarrow{OP},\overrightarrow{AB}$,代入数量积公式计算.
解答 解:(1)∵$\overrightarrow{BP}$=2$\overrightarrow{PA}$,∴$\overrightarrow{BP}$=$\frac{2}{3}$$\overrightarrow{BA}$=$\frac{2}{3}$($\overrightarrow{OA}-\overrightarrow{OB}$)=$\frac{2}{3}\overrightarrow{OA}-\frac{2}{3}\overrightarrow{OB}$,∴$\overrightarrow{OP}$=$\overrightarrow{OB}+\overrightarrow{BP}$=$\frac{2}{3}\overrightarrow{OA}$+$\frac{1}{3}\overrightarrow{OB}$∴x=$\frac{2}{3}$,y=$\frac{1}{3}$.
(2)∵$\overrightarrow{BP}$=3$\overrightarrow{PA}$,∴$\overrightarrow{BP}$=$\frac{3}{4}$$\overrightarrow{BA}$=$\frac{3}{4}$$\overrightarrow{OA}$-$\frac{3}{4}$$\overrightarrow{OB}$,∴$\overrightarrow{OP}$=$\overrightarrow{OB}$+$\overrightarrow{BP}$=$\frac{3}{4}$$\overrightarrow{OA}$+$\frac{1}{4}$$\overrightarrow{OB}$,
∵$\overrightarrow{OA}•\overrightarrow{OB}$=4×2×cos60°=4.$\overrightarrow{AB}$=$\overrightarrow{OB}-\overrightarrow{OA}$,$\overrightarrow{OA}$2=16,$\overrightarrow{OB}$2=4,
∴$\overrightarrow{OP}$•$\overrightarrow{AB}$=($\frac{3}{4}$$\overrightarrow{OA}$+$\frac{1}{4}$$\overrightarrow{OB}$)•($\overrightarrow{OB}-\overrightarrow{OA}$)=-$\frac{3}{4}$$\overrightarrow{OA}$2$+\frac{1}{2}$$\overrightarrow{OA}•\overrightarrow{OB}$+$\frac{1}{4}$$\overrightarrow{OB}$2=-$\frac{3}{4}$×16+$\frac{1}{2}$×4+$\frac{1}{4}$×4=-9.
点评 本题考查了平面向量的基本道理,向量的数量积运算,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n(3n-1) | B. | $\frac{n(n+3)}{2}$ | C. | n(n+1) | D. | $\frac{n(3n+1)}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有一个零点 | B. | 有两个零点 | C. | 可能没有零点 | D. | 以上说法不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{19}{13}$ | B. | $\frac{20}{13}$ | C. | $\frac{21}{13}$ | D. | $\frac{22}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{5π}{6}$,0) | B. | ($\frac{π}{3}$,0) | C. | ($\frac{π}{6}$,0) | D. | (-$\frac{π}{3}$,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com