练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．“（x-1）（x+2）=0”是“x=1”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    分析 根据充分条件和必要条件的定义进行判断即可．

    解答 解：由（x-1）（x+2）=0得x=1或x=-2，
    则“（x-1）（x+2）=0”是“x=1”的必要不充分条件，
    故选：B

    点评 本题主要考查充分条件和必要条件的判断，根据充分条件和必要条件的定义是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．已知函数$f（x）=\left\{\begin{array}{l}（{4a-3}）x+2a-4，x≤t\\ 2{x^3}-6x，x＞t\end{array}\right.$，无论t取何值，函数f（x）在R上总是不单调，则实数a的取值范围是（　　）
    A．（-∞，1）B．$[{\frac{1}{4}，+∞}）$C．$[{\frac{3}{4}，+∞}）$D．$（{-∞，\frac{3}{4}}]$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

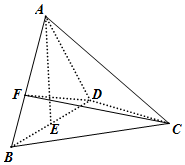    20．如图，在三棱锥A-BCD中，已知△ABD，△BCD都是边长为2的等边三角形，E为BD中点，且AE⊥平面BCD，F为线段AB上一动点，记$\frac{BF}{BA}=λ$．
    （1）当$λ=\frac{1}{3}$时，求异面直线DF与BC所成角的余弦值；
    （2）当CF与平面ACD所成角的正弦值为$\frac{{\sqrt{15}}}{10}$时，求λ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知$\frac{π}{4}＜x＜\frac{π}{2}$，设a=sinx，b=cosx，c=tanx，则（　　）
    A．a＜b＜cB．b＜a＜cC．a＜c＜bD．b＜c＜a

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

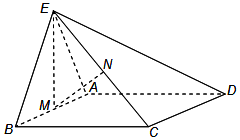    4．如图，正三角形ABE与菱形ABCD所在的平面互相垂直，AB=2，∠ABC=60°，M是AB的中点，N是CE的中点．
    （I）求证：EM⊥AD；
    （II）求证：MN∥平面ADE；
    （III）求点A到平面BCE的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知函数$y=\frac{3+x}{x-2}，x∈[3，6]$
    （1）判断并证明函数的单调性；
    （2）求此函数的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知e是自然对数的底数，函数f（x）=（ax2+x）ex，若f（x）在[-1，1]上是单调增函数，则a的取值范围是（　　）
    A．[-$\frac{2}{3}$，0]B．（-∞，0）∪[$\frac{2}{3}$，+∞）C．[0，$\frac{2}{3}$]D．（-∞，-$\frac{2}{3}$]∪[0，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

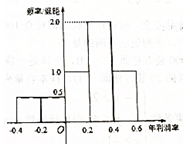    18．某公司计划明年用不超过6千万元的资金投资于本地养鱼场和远洋捕捞队．经过本地养鱼场年利润率的调研，得到如图所示年利润率的频率分布直方图．对远洋捕捞队的调研结果是：年利润率为60%的可能性为0.6，不赔不赚的可能性为0.2，亏损30%的可能性为0.2．假设该公司投资本地养鱼场的资金为x（x≥0）千万元，投资远洋捕捞队的资金为y（y≥0）千万元．
    （1）利用调研数据估计明年远洋捕捞队的利润ξ的分布列和数学期望Eξ．
    （2）为确保本地的鲜鱼供应，市政府要求该公司对本地养鱼场的投资不得低于远洋捕捞队的一半．适用调研数据，给出公司分配投资金额的建议，使得明年两个项目的利润之和最大．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知点P在圆C：x2+y2=4上，而Q为P在x轴上的投影，且点N满足$\overrightarrow{PN}=\overrightarrow{NQ}$，设动点N的轨迹为曲线E．
    （1）求曲线E的方程；
    （2）若A，B是曲线E上两点，且|AB|=2，O为坐标原点，求△AOB的面积的最大值．

    查看答案和解析>>

    同步练习册答案