
| A. | 2 | B. | 4 | C. | 1 | D. | 3 |
分析 利用三角函数的诱导公式及同角三角函数的基本关系式化简,求得函数周期判断(1);由f(x1)=-f(x2)得到x1与x2的关系判断(2);由f(-$\frac{π}{4}$)为函数最小值判断(3);由复合函数的单调性判断(4).
解答 解:$f(x)=sin(x+\frac{3π}{2})cos(\frac{π}{2}+x)$=-cosx•(-sinx)=sinxcosx=$\frac{1}{2}sin2x$.
(1)函数f(x)的最小正周期为π,正确;
(2)若f(x1)=-f(x2),则$\frac{1}{2}sin2{x}_{1}=-\frac{1}{2}sin2{x}_{2}=\frac{1}{2}sin(-2{x}_{2})$,
∴2x1=-2x2+2kπ(k∈Z)或2x1-2x2=π+2kπ(k∈Z),故(2)错误;
(3)∵$f(-\frac{π}{4})=\frac{1}{2}sin[2×(-\frac{π}{4})]=-\frac{1}{2}$,∴f(x)的图象关于直线$x=-\frac{π}{4}$对称,故(3)正确;
(4)由x∈$[{\frac{π}{4},\frac{3π}{4}}]$,得2x∈$[\frac{π}{2},\frac{3π}{2}]$,得f(x)在$[{\frac{π}{4},\frac{3π}{4}}]$上是减函数,故(4)正确.
∴其中正确命题的个数是3个.
故选:D.
点评 本题考查命题的真假判断与应用,考查了三角函数的诱导公式、同角三角函数的基本关系式及y=Asin(ωx+φ)型函数的图象和性质,是中档题.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-12,1] | B. | [-12,0] | C. | [-2,4] | D. | [1,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知等腰梯形ABCD中,AD∥BC,BC=2AD=2AB=4,将△ABD沿BD折到△A′BD的位置,使平面A′BD⊥平面CBD.
如图,已知等腰梯形ABCD中,AD∥BC,BC=2AD=2AB=4,将△ABD沿BD折到△A′BD的位置,使平面A′BD⊥平面CBD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
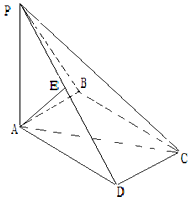 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=90°,四边形ABCD是平行四边形,且PA=AD=2,AB=1,E是线段PD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=90°,四边形ABCD是平行四边形,且PA=AD=2,AB=1,E是线段PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com