
 如图,已知等腰梯形ABCD中,AD∥BC,BC=2AD=2AB=4,将△ABD沿BD折到△A′BD的位置,使平面A′BD⊥平面CBD.
如图,已知等腰梯形ABCD中,AD∥BC,BC=2AD=2AB=4,将△ABD沿BD折到△A′BD的位置,使平面A′BD⊥平面CBD.分析 (I)法一:由余弦定理推导出BD⊥CD,从而CD⊥面A'BD,由此能证明A'B⊥CD.
法二:过点A作AE⊥BC于E,过点D作DF⊥BC于F,则AE∥DF,推导出CD⊥BD,从而CD⊥平面A'BD,由此能证明CD⊥A'B.
(II)法一:取BD的中点O,连接A′O,推导出平面A'OC⊥平面BCD,过点P作PQ⊥OC于Q,则PQ⊥平面BCD,过点Q作QH⊥BD于H,连接PH,推导出PH⊥BD,从而∠PHQ为二面角P-BD-C的平面角,由此能求出P为A'C上靠近A'的三等分点,二面角P-BD-C的大小为45°.
法二:以D为坐标原点,以$\overrightarrow{DB}$的方向为x轴正方向,建立空间直角坐标系D-xyz,利用向量法能求出点P在线段A'C靠近A'的三等分点处.
解答 证明:(I)证法一:在△ABC中,由余弦定理得BD2=AB2+AD2-2AB•ADcosA=4+4+8cosC,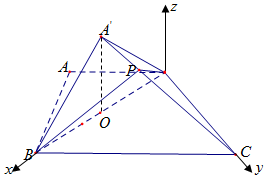
在△BCD中,由余弦定理得BD2=BC2+CD2-2BC•CD•cosC=16+4-16cosC
由上述两式可知,$BD=2\sqrt{3},cosC=\frac{1}{2}$(3分)
∴BD⊥CD(4分)
又∵面A'BD⊥面CBD,面A'BD∩面CBD=BD,
∴CD⊥面A'BD(5分)
∵A'B?面A'BD,∴A'B⊥CD.(6分)
解:(II)法一:存在.P为A'C上靠近A'的三等分点.(7分)
取BD的中点O,连接A′O,∵A'B=A'D∴A'O⊥BD
又∵平面A′BD⊥平面CBD,∴A'O⊥平面CBD,(8分)
∴平面A'OC⊥平面BCD,
过点P作PQ⊥OC于Q,则PQ⊥平面BCD,过点Q作QH⊥BD于H,连接PH.
则QH是PH在平面BDC的射影,故PH⊥BD,
所以,∠PHQ为二面角P-BD-C的平面角,(10分)
P为A'C上靠近A'的三等分点,
∴$PQ=\frac{2}{3}$,$\frac{OQ}{OC}=\frac{1}{3}$,∴$HQ=\frac{1}{3}DC=\frac{2}{3}$,∴∠PHD=45°.
∴二面角P-BD-C的大小为45°. (12分)
证明:(Ⅰ)证法一:在等腰梯形ABCD中,过点A作AE⊥BC于E,
过点D作DF⊥BC于F,则AE∥DF,∴EF=AD=2,
又∵在等腰梯形ABCD中,Rt△ABE≌Rt△DCF且BC=4∴BE=FC=1∴$cosC=\frac{1}{2}$D(2分)
在△BCD中,$B{D^2}=B{C^2}+C{D^2}-2BC•CD•cosC={4^2}+{2^2}-2×4×2×\frac{1}{2}=12$,
∴BD2+CD2=BC2,∴CD⊥BD,(4分)
又∵平面A'BD⊥平面CBD,
面A'BD∩面CBD=BD∴CD⊥平面A'BD(5分)∴CD⊥A'B.(6分)
(Ⅱ)解法二:由(Ⅰ)知CD⊥BD,CD⊥平面A′BD.
以D为坐标原点,以$\overrightarrow{DB}$的方向为x轴正方向,建立如图所示的空间直角坐标系D-xyz.(7分)
则D(0,0,0),$B(2\sqrt{3},0,0)$,C(0,2,0),
取BD的中点O,连接A'O,∵A'B=A'D∴A'O⊥BD
在等腰△A'BD中$A'B=2,BD=2\sqrt{3}$可求得A'O=1∴$A'(\sqrt{3},0,1)$(8分)
所以$\overrightarrow{DB}=(2\sqrt{3},0,0)$,$\overrightarrow{BA'}=(-\sqrt{3},0,1)$$\overrightarrow{A'C}=(-\sqrt{3},2,-1)$
设$\overrightarrow{A'P}=λ\overrightarrow{A'C}$,则$\overrightarrow{BP}=\overrightarrow{BA'}+\overrightarrow{A'P}=(-\sqrt{3}-\sqrt{3}λ,2λ,1-λ)$
设$\overrightarrow n=(x,y,z)$是平面PBD的法向量,则$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{BP}=0\\ \overrightarrow n•\overrightarrow{DB}=0\end{array}\right.$,
即$\left\{\begin{array}{l}(-\sqrt{3}-\sqrt{3}λ)x+2λy+(1-λ)z=0\\ 2\sqrt{3}x=0\end{array}\right.$可取$\overrightarrow n=(0,\frac{λ-1}{2λ},1)$
易知:平面CBD的一个法向量为$\overrightarrow m=(0,0,1)$(10分)
由已知二面角P-BD-C的大小为45°.
∴$|cos<\overrightarrow m,\overrightarrow n>|=\frac{\overrightarrow m•\overrightarrow n}{{|\overrightarrow{m|}•|\overrightarrow n|}}=\frac{1}{{\sqrt{{{(\frac{λ-1}{2λ})}^2}+1}}}=\frac{{\sqrt{2}}}{2}$,
解得:$λ=\frac{1}{3}$或λ=-1(舍)
∴点P在线段A'C靠近A'的三等分点处. (12分)
点评 本题考查线线垂直的证明,考查满足条件的点的位置的确定与求法,考查空间中线线、线面、面面间的位置关系,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想,是中档题.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{\sqrt{2}}{2}$,1) | B. | ($\frac{1}{2}$,1) | C. | (0,$\frac{\sqrt{2}}{2}$) | D. | (0,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | B. | $\frac{y^2}{4}-\frac{x^2}{12}=1$ | C. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ | D. | $\frac{y^2}{12}-\frac{x^2}{4}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com