
| A. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | B. | $\frac{y^2}{4}-\frac{x^2}{12}=1$ | C. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ | D. | $\frac{y^2}{12}-\frac{x^2}{4}=1$ |
分析 根据题意,求出椭圆$\frac{x^2}{9}+\frac{y^2}{25}=1$的焦点坐标以及离心率e,由此设双曲线的方程为$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1,由题意可得a2+b2=16以及e=$\frac{c}{a}$=$\frac{5}{4}$,解可得a2=4,b2=12,代入双曲线的方程即可得答案.
解答 解:根据题意,椭圆的方程为$\frac{x^2}{9}+\frac{y^2}{25}=1$,
其焦点坐标为(0,±4),离心率e=$\frac{4}{5}$,
对于双曲线,设其方程为$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1,
则有a2+b2=16,
且其离心率e=$\frac{c}{a}$=$\frac{5}{4}$,
解可得a2=4,b2=12,
则双曲线的方程为:$\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{12}$=1;
故选:B.
点评 本题考查双曲线、椭圆的标准方程,关键是求出椭圆的焦点坐标以及离心率.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案科目:高中数学 来源: 题型:解答题
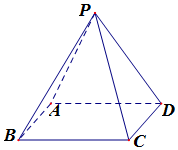 如图在四棱锥P-ABCD中,底面ABCD为矩形,侧面PAD⊥底面ABCD,PA⊥PC;
如图在四棱锥P-ABCD中,底面ABCD为矩形,侧面PAD⊥底面ABCD,PA⊥PC;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若q>1,则数列{Tn}单调递增 | B. | 若数列{Tn}单调递增,则q>1 | ||
| C. | 若Tn>0,则数列{Tn}单调递增 | D. | 若数列{Tn}单调递增,则Tn>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知等腰梯形ABCD中,AD∥BC,BC=2AD=2AB=4,将△ABD沿BD折到△A′BD的位置,使平面A′BD⊥平面CBD.
如图,已知等腰梯形ABCD中,AD∥BC,BC=2AD=2AB=4,将△ABD沿BD折到△A′BD的位置,使平面A′BD⊥平面CBD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -9 | B. | $-\frac{7}{3}$ | C. | $-\frac{2}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
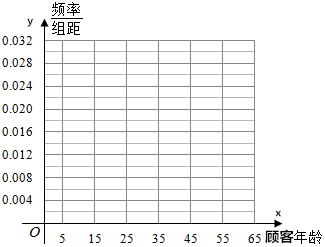 某电商在6月18日之后,随机抽取100名顾客进行回访,按顾客的年龄分成6组,得到如下频数分布表:
某电商在6月18日之后,随机抽取100名顾客进行回访,按顾客的年龄分成6组,得到如下频数分布表:| 顾客年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65] |
| 频数 | 4 | 24 | 32 | 20 | 16 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com