
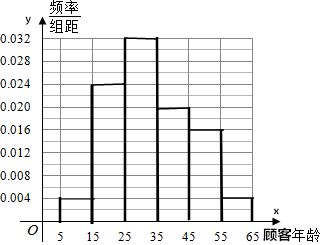
 ij������6��18��֮�������ȡ100���˿ͽ��лطã����˿͵�����ֳ�6�飬�õ�����Ƶ���ֲ�����
ij������6��18��֮�������ȡ100���˿ͽ��лطã����˿͵�����ֳ�6�飬�õ�����Ƶ���ֲ�����| ���˿����� | [5��15�� | [15��25�� | [25��35�� | [35��45�� | [45��55�� | [55��65] |
| ��Ƶ�� | ��4 | ��24 | ��32 | ��20 | ��16 | ��4 |
���� ��1�����ݱ������ݣ���Ƶ�ʷֲ���������Ƶ�ʷֲ�ֱ��ͼ��
��2������Ƶ�ʷֲ�ֱ��ͼ������˿������ƽ������
��3�������ȡ��25����������[25��35���ڵĹ˿��������Լ��������X�Ŀ���ȡֵ��
�����Ӧ�ĸ��ʣ�д��X�ķֲ��У�������ѧ����ֵ��
��� �⣺��1�����ݱ������ݣ���Ƶ�ʷֲ������£�
| �˿����� | [5��15�� | [15��25�� | [25��35�� | [35��45�� | [45��55�� | [55��65] | �ϼ� |
| ��Ƶ�� | ��4 | ��24 | ��32 | ��20 | ��16 | ��4 | 100 |
| Ƶ�� | 0.04 | 0.24 | 0.32 | 0.20 | 0.16 | 0.04 | 1.00 |
| $\frac{Ƶ��}{���}$ | 0.004 | 0.024 | 0.032 | 0.020 | 0.016 | 0.004 | 0.10 |
| X | 0 | 1 | 2 |
| P | $\frac{34}{75}$ | $\frac{34}{75}$ | $\frac{7}{75}$ |
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ�Լ���ɢ����������ķֲ�������ѧ�����ļ������⣬���е��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | B�� | $\frac{y^2}{4}-\frac{x^2}{12}=1$ | C�� | $\frac{x^2}{12}-\frac{y^2}{4}=1$ | D�� | $\frac{y^2}{12}-\frac{x^2}{4}=1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com