
分析 ①a=3,对于q:(x-2)(x-3)<0,解得2<x<3.即可判断出p与q的关系.
②a>2时,对于q:(x-2)(x-a)<0,解得2<x<a.可得p是q的必要不充分条件条件.舍去.a<2时,对于q:(x-2)(x-a)<0,解得a<x<2.对a分类讨论:a<1,1≤a<2,即可的判断出关系.
解答 解:①a=3,对于q:(x-2)(x-3)<0,解得2<x<3.则p是q的必要不充分条件.
②a>2时,对于q:(x-2)(x-a)<0,解得2<x<a.则p是q的必要不充分条件条件.舍去.
a<2时,对于q:(x-2)(x-a)<0,解得a<x<2.
若a<1,则p既不是q的充分条件,也不是q必要条件,满足条件.
若1≤a<2,则p是q的必要不充分条件条件.舍去.
综上可得:a的取值范围是(-∞,1).
故答案为:必要不充分条件,(-∞,1).
点评 本题考查了不等式的解法、分类讨论方法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -9 | B. | $-\frac{7}{3}$ | C. | $-\frac{2}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 任意m∈A,都有f(m+3)>0 | B. | 任意m∈A,都有f(m+3)<0 | ||
| C. | 存在m∈A,都有f(m+3)=0 | D. | 存在m∈A,都有f(m+3)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
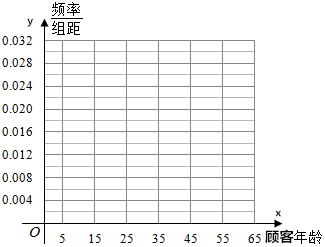 某电商在6月18日之后,随机抽取100名顾客进行回访,按顾客的年龄分成6组,得到如下频数分布表:
某电商在6月18日之后,随机抽取100名顾客进行回访,按顾客的年龄分成6组,得到如下频数分布表:| 顾客年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65] |
| 频数 | 4 | 24 | 32 | 20 | 16 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com