
分析 (1)根据题意,由向量$\overrightarrow{a}$、$\overrightarrow{b}$的坐标,由向量的加法坐标计算公式,计算即可得答案;
(2)根据题意,求出$\overrightarrow{m}$的坐标,由向量平行的坐标表示公式可得2(λ+2)=λ+5,解可得λ的值,即可得答案.
解答 解:(1)因为$\overrightarrow a=(2,1)$,$\overrightarrow b=(1,1)$,所以$\overrightarrow a+\overrightarrow b=(2,1)+(1,1)=(3,2)$.
(2)因为$\overrightarrow b=(1,1)$,$\overrightarrow c=(5,2)$,所以$\overrightarrow m=λ\overrightarrow b+\overrightarrow c=λ(1,1)+(5,2)=(λ+5,λ+2)$.
又因为$\overrightarrow a=(2,1)$,且$\overrightarrow a$与$\overrightarrow m$平行,所以2(λ+2)=λ+5,解得λ=1.
点评 本题考查向量平行的坐标表示,涉及向量的坐标运算,关键是掌握向量坐标计算的公式.


科目:高中数学 来源: 题型:选择题
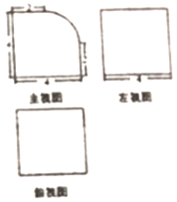
| A. | 64-4π | B. | 64+6π | C. | 48+4π | D. | 64-6π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | 3 | C. | 8 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [9,11] | B. | [9,12] | C. | [9,13] | D. | [9,14] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,0<φ<π)的图象如图所示,
函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,0<φ<π)的图象如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
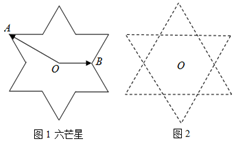 如图2,“六芒星”是由两个全等正三角形组成,中心重合于点O且三组对边分别平行.点A,B是“六芒星”(如图1)的两个顶点,动点P在“六芒星”上(内部以及边界),若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,则x+y的取值范围是( )
如图2,“六芒星”是由两个全等正三角形组成,中心重合于点O且三组对边分别平行.点A,B是“六芒星”(如图1)的两个顶点,动点P在“六芒星”上(内部以及边界),若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,则x+y的取值范围是( )| A. | [-4,4] | B. | $[{-\sqrt{21},\sqrt{21}}]$ | C. | [-5,5] | D. | [-6,6] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com