Question

9．等腰直角三角形ABC中，∠C=90°，AC=BC=1，点M，N分别是AB，BC中点，点P是△ABC（含边界）内任意一点，则$\overrightarrow{AN}$•$\overrightarrow{MP}$的取值范围是（　　）

• A． [-$\frac{3}{4}$，$\frac{3}{4}$]
• B． [-$\frac{1}{4}$，$\frac{3}{4}$]
• C． [-$\frac{3}{4}$，$\frac{1}{4}$]
• D． [$\frac{1}{4}$，$\frac{3}{4}$]

Answer 1

分析 选择合适的原点建立坐标系，分别给出动点（含参数）和定点的坐标，结合向量内积计算公式进行求解．

解答 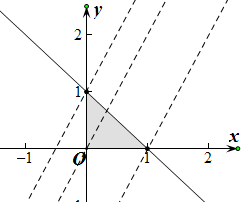解：以C为坐标原点，CA边所在直线为x轴，
建立直角坐标系，
则A（1，0），B（0，1），
设P（x，y），
则$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y-1≤0}\end{array}\right.$
且$\overrightarrow{AN}$=（-1，$\frac{1}{2}$），$\overrightarrow{MP}$=（x-$\frac{1}{2}$，y-$\frac{1}{2}$），
则$\overrightarrow{AN}$•$\overrightarrow{MP}$=-x+$\frac{1}{2}$y+$\frac{1}{4}$，
令t=-x+$\frac{1}{2}$y+$\frac{1}{4}$，结合线性规划知识，
则y=2x+2t-$\frac{1}{2}$
当直线t=-x+$\frac{1}{2}$y+$\frac{1}{4}$经过点A（1，0）时，$\overrightarrow{AN}$•$\overrightarrow{MP}$有最小值，
将（1，0）代入得t=-$\frac{3}{4}$，
当直线t=-x+$\frac{1}{2}$y+$\frac{1}{4}$经过点B时，$\overrightarrow{AN}$•$\overrightarrow{MP}$有最大值，
将（0，1）代入得t=$\frac{3}{4}$，
则$\overrightarrow{AN}$•$\overrightarrow{MP}$的取值范围是[-$\frac{3}{4}$，$\frac{3}{4}$]，
故选：A

点评 本题考查的知识点是平面向量的数量积运算及线性规划，处理的关键是建立恰当的坐标系，求出各点、向量的坐标，利用平面向量的数量积公式，将其转化为线性规划问题，再利用“角点法”解决问题．