
分析 利用辅助角公式化简函数的解析式,再利用正弦函数的图象的周期性和对称性,可得|$\frac{π}{5a}$|=$\frac{π}{3}$,由此求得实数a的值.
解答 解:∵函数f(x)=4sin5ax-4$\sqrt{3}$cos5ax
=8($\frac{1}{2}$sin5ax-$\frac{\sqrt{3}}{2}$cos5ax)=8sin(5ax-$\frac{π}{3}$)的图象的相邻两条对称轴之间的距离为|$\frac{π}{5a}$|=$\frac{π}{3}$,
∴a=±$\frac{3}{5}$,
故答案为:$±\frac{3}{5}$.
点评 本题主要考查辅助角公式,正弦函数的图象的周期性和对称性,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | -2016 | C. | 2017 | D. | -2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{3}{4}$,$\frac{3}{4}$] | B. | [-$\frac{1}{4}$,$\frac{3}{4}$] | C. | [-$\frac{3}{4}$,$\frac{1}{4}$] | D. | [$\frac{1}{4}$,$\frac{3}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | [-2,+∞) | C. | (-3,+∞) | D. | (-$\frac{9}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -12 | B. | -6 | C. | 12 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x<1} | B. | {-1,0,1} | C. | {-1,0} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
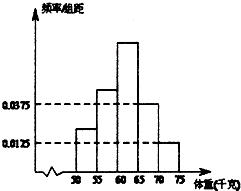 为了解某校高三毕业生报考体育专业学生的体重(单位:千克),将他们的体重数据整理后得到如下频率分布直方图,已知图中从左到右前3个小组的频率之比为1:2:3,其中第二小组的频数为8.
为了解某校高三毕业生报考体育专业学生的体重(单位:千克),将他们的体重数据整理后得到如下频率分布直方图,已知图中从左到右前3个小组的频率之比为1:2:3,其中第二小组的频数为8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com