
���� ��1��������C�IJ�������Ϊ$\left\{\begin{array}{l}{x=4cos��}\\{y=cos2��}\end{array}\right.$����Ϊ�����������ñ��ǹ�ʽ�ɵ�y=cos2��=2cos2��-1=$2����\frac{x}{4}��^{2}$-1�����������ɵ�����C����ͨ���̣�ע��x��ȡֵ��Χ��
��2��ֱ��l����ͨ����Ϊx-y+3=0�����õ㵽ֱ�ߵľ��빫ʽ�ɵã�����C�ϵĵ㵽l�ľ���d=$\frac{|4cos��-cos2��+3|}{\sqrt{2}}$=$\frac{|2��cos��-1��^{2}-6|}{\sqrt{2}}$�����ɵó���
��� �⣺��1��������C�IJ�������Ϊ$\left\{\begin{array}{l}{x=4cos��}\\{y=cos2��}\end{array}\right.$����Ϊ��������
��y=cos2��=2cos2��-1=$2����\frac{x}{4}��^{2}$-1��
��Ϊy=$\frac{{x}^{2}}{8}$-1��cos�ȡ�[-1��1]���ɵ�x��[-1��1]��
������C����ͨ����Ϊ��y=$\frac{{x}^{2}}{8}$-1��x��[-1��1]��
��2��ֱ��l����ͨ����Ϊx-y+3=0������C�ϵĵ㵽l�ľ���d=$\frac{|4cos��-cos2��+3|}{\sqrt{2}}$=$\frac{|2��cos��-1��^{2}-6|}{\sqrt{2}}$��$\frac{6}{\sqrt{2}}$=3$\sqrt{2}$��
��cos��=1ʱ��dȡ�����ֵ3$\sqrt{2}$��
���� ���⿼���˲������̻�Ϊ��ͨ���̡����ǹ�ʽ���Ͳʽ���㵽ֱ�ߵľ��빫ʽ��������������������������������е��⣮


 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪������P-ABCD�У�����ABCD��ƽ���ı��Σ�PA��ƽ��ABCD��PA=$\sqrt{3}$��AB=1��AD=2����BAD=120�㣬E��G��H�ֱ���BC��PC��AD���е㣮
��ͼ����֪������P-ABCD�У�����ABCD��ƽ���ı��Σ�PA��ƽ��ABCD��PA=$\sqrt{3}$��AB=1��AD=2����BAD=120�㣬E��G��H�ֱ���BC��PC��AD���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}x=2x'\\ y=3y'\end{array}\right.$ | B�� | .$\left\{\begin{array}{l}x=\frac{1}{2}x'\\ y=\frac{1}{3}y'\end{array}\right.$ | C�� | .$\left\{\begin{array}{l}x=4x'\\ y=9y'\end{array}\right.$ | D�� | .$\left\{\begin{array}{l}x=\frac{1}{4}x'\\ y=\frac{1}{9}y'\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
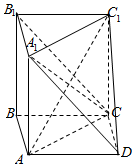 ��ͼ��ʾ�ļ������У�������ABC-A1B1C1Ϊֱ��������ABCDΪƽ���ı��Σ�AD=2CD����ADC=60�㣮
��ͼ��ʾ�ļ������У�������ABC-A1B1C1Ϊֱ��������ABCDΪƽ���ı��Σ�AD=2CD����ADC=60�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{2}}{2}$ | B�� | $\sqrt{2}$ | C�� | $\sqrt{3}$ | D�� | $\frac{\sqrt{6}}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com