
| A. | 4 | B. | 3 | C. | 5 | D. | 6 |
分析 将x换为x+3,可得f(x+6)=f(x),则f(x)为最小正周期为6的函数,由f(3-x)=f(x-3),将x换为3-x,可得f(x)=f(-x),即f(x)为偶函数,作出函数y=2log3(2x+3)和f(x)在(0,2016)的图象,由2log333>f(15),可得方程在区间(0,2016)内解的个数.
解答  解:由f(x-3)=f(x+3),
解:由f(x-3)=f(x+3),
将x换为x+3,
可得f(x+6)=f(x),
则f(x)为最小正周期为6的函数,
又f(3-x)=f(3+x),可得
f(3-x)=f(x-3),
将x换为3-x,可得f(x)=f(-x),
即f(x)为偶函数,
由x∈[-3,0]时.f(x)=2-x-2,
可得x∈[0,3]时.f(x)=2x-2,
由f(x)在[-3,0]递减,可得f(x)≤f(-3)=6,
画出函数y=2log3(2x+3)的图象,可得函数y在(0,2016)递增,
运用周期函数的图象画法,可得f(x)在(0,2016)的图象,
由f(15)=f(15-12)=f(3)=f(-3)=6,
而2log333>6,可得方程f(x)-2log3(2x+3)=0
在区间(0,2016)内解的个数是4.
故选:A.
点评 本题考查方程的解的个数的解法,注意运用函数的图象的交点个数,同时考查函数的周期性和奇偶性、对称性的运用,考查化简整理的运算能力和数形结合的能力,属于中档题.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:选择题
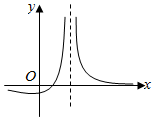 函数f(x)=$\frac{ax-b}{{{{(x-c)}^2}}}$的图象如图所示,则下列结论成立的是( )
函数f(x)=$\frac{ax-b}{{{{(x-c)}^2}}}$的图象如图所示,则下列结论成立的是( )| A. | a>0,b>0,c>0 | B. | a<0,b<0,c>0 | C. | a>0,b>0,c<0 | D. | a<0,b>0,c>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 品质 季节 | 优质品数量 | 合格品数量 |
| 夏秋季生产 | 26 | 8 |
| 春冬季生产 | 12 | 4 |
 | B1 | B2 |
| A1 | a | b |
| A2 | c | d |
| p(x2≥k0) | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{\sqrt{15}}{4}$ | D. | -$\frac{\sqrt{15}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
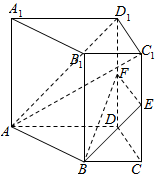 已知直四棱柱ABCD-A1B1C1D1,AD=DD1=2,BC=DC=1,DC⊥BC,AD∥BC,E,F分别为CC1,DD1的中点.
已知直四棱柱ABCD-A1B1C1D1,AD=DD1=2,BC=DC=1,DC⊥BC,AD∥BC,E,F分别为CC1,DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 3或4 | D. | 4或5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com