
分析 (Ⅰ)设切点为(m,n),即有n=bm=em-1,求得F(x)的导数,运用导数的几何意义,可得m,b的方程,构造函数g(b)=blnb-b+1,求得导数,单调区间可得极值,进而得到b=1;
(Ⅱ)求得f(x)的解析式和导数,设g(x)=f′(x),设x0为f(x)在区间(0,1)内的一个零点,运用单调性,讨论a的范围,结合零点存在定理,即可得证.
解答 解:(Ⅰ)a=0时,y=G(x)=bx,
F(x)=ex-1的导数为F′(x)=ex,
设切点为(m,n),即有n=bm=em-1,
且em=b,消去m,可得blnb=b-1,
设g(b)=blnb-b+1,g′(b)=lnb,
当b>1时,g′(b)>0,g(b)递增;
当0<b<1时,g′(b)<0,g(b)递减.
可得b=1处g(b)取得极小值,且为最小值0.
则blnb=b-1的解为b=1;
(Ⅱ)证明:f(x)=F(x)-G(x)=ex-1-ax2-bx,
可得f′(x)=ex-2ax-b,可设g(x)=f′(x),
设x0为f(x)在区间(0,1)内的一个零点,
由f(0)=f(x0)=0可知,
f(x)在区间(0,x0)上不可能单调递增,也不可能单调递减.
则g(x)不可能恒为正,也不可能恒为负.
故g(x)在区间(0,x0)内存在零点x1.
同理g(x)在区间(x0,1)内存在零点x2.
故g(x)在区间(0,1)内至少有两个零点,
由(1)知,当a≤$\frac{1}{2}$时,g(x)在[0,1]递增,
故g(x)在(0,1)内至多有1个零点,
当a≥$\frac{e}{2}$时,g(x)在[0,1]递减,
故g(x)在(0,1)内至多有1个零点,都不合题意,
所以$\frac{1}{2}$<a<$\frac{e}{2}$,
此时,g(x)在区间[0,ln(2a)]递减,在区间(ln(2a),1)递增,
因此x1∈(0,ln(2a)),x2∈(ln(2a),1),必有:g(0)=1-b>0,g(1)=e-2a-b>0,
由f(1)=0,得a+b=e-1<2,有g(0)=a-e+2>0,g(1)=1-a>0,解得:e-2<a<1,
所以当e-2<a<1时,函数f(x)在区间(0,1)内有零点.
点评 本题考查导数的运用:求切线的斜率和单调区间,考查函数的单调性,函数的最值问题,以及分类讨论思想,是一道综合题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:选择题
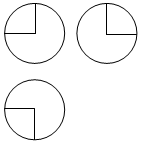 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是$\frac{28π}{3}$,则它的表面积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是$\frac{28π}{3}$,则它的表面积是( )| A. | 17π | B. | 18π | C. | 20π | D. | 28π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{8}{25}$ | D. | $\frac{9}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
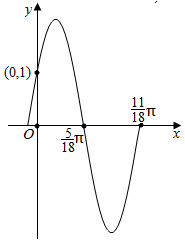
| A. | $\sqrt{3}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
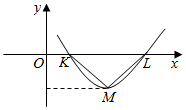 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则f($\frac{1}{12}$)的值为( )
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则f($\frac{1}{12}$)的值为( )| A. | $\frac{\sqrt{6}-\sqrt{2}}{8}$ | B. | $\frac{\sqrt{2}+\sqrt{6}}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{3}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com