
分析 设椭圆上两点A(x1,y1)、B(x2,y2)关于直线y=4x+m对称,AB中点为M(x0,y0),利用点差法与直线y=4x+m可求得x0=-m,y0=-3m,点M(x0,y0)在椭圆内部,将其坐标代入椭圆方程即可求得m的取值范围.
解答 解:∵椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,即有3x2+4y2-12=0,
设椭圆上两点A(x1,y1)、B(x2,y2)关于直线y=4x+m对称,AB中点为M(x0,y0),
则3x12+4y12=12,①
3x22+4y22=12 ②
①-②得:3(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0,
即 3•2x0•(x1-x2)+4•2y0•(y1-y2)=0,
∴kAB=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{3}{4}$•$\frac{{x}_{0}}{{y}_{0}}$=-$\frac{1}{4}$.
∴y0=3x0,代入直线方程y=4x+m得x0=-m,y0=-3m;
因为(x0,y0)在椭圆内部,
∴3m2+4•(-3m)2<12,即3m2+36m2<12,
解得-$\frac{2\sqrt{13}}{13}$<m<$\frac{2\sqrt{13}}{13}$.
故答案为:-$\frac{2\sqrt{13}}{13}$<m<$\frac{2\sqrt{13}}{13}$.
点评 本题考查直线与椭圆的综合问题,着重考查点差法的应用,突出化归思想的考查,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
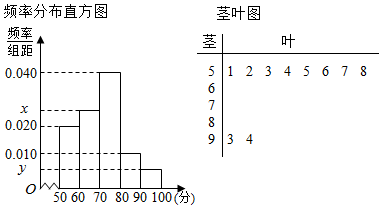
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
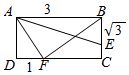 在矩形ABCD中,AB=3,BC=$\sqrt{3}$,$\overrightarrow{BE}=2\overrightarrow{EC}$,点F在边CD上,若$\overrightarrow{AB}•\overrightarrow{AF}=3$,则$\overrightarrow{AE}•\overrightarrow{BF}$的值为( )
在矩形ABCD中,AB=3,BC=$\sqrt{3}$,$\overrightarrow{BE}=2\overrightarrow{EC}$,点F在边CD上,若$\overrightarrow{AB}•\overrightarrow{AF}=3$,则$\overrightarrow{AE}•\overrightarrow{BF}$的值为( )| A. | 4 | B. | $\frac{8\sqrt{3}}{3}$ | C. | 0 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{3}$,$\frac{2}{3}$) | B. | [$\frac{1}{3}$,$\frac{2}{3}$) | C. | ($\frac{1}{2}$,$\frac{2}{3}$) | D. | [$\frac{1}{2}$,$\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -2 | C. | -16 | D. | 1或-16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com