Question

10．以下命题正确的是：①③④．
①把函数y=3sin（2x+$\frac{π}{3}$）的图象向右平移$\frac{π}{6}$个单位，可得到y=3sin2x的图象；
②四边形ABCD为长方形，AB=2，BC=1，O为AB中点，在长方形ABCD内随机取一点P，取得的P点到O的距离大于1的概率为1-$\frac{π}{2}$；
③某校开设A类选修课3门，B类选择课4门，一位同学从中共选3门，若要求两类课程中各至少选一门，则不同的选法共有30种；
④在某项测量中，测量结果ξ服从正态分布N（2，σ²）（σ＞0）．若ξ在（-∞，1）内取值的概率为0.1，则ξ在（2，3）内取值的概率为0.4．

Answer 1

分析 ①根据三角函数的图象平移关系进行判断．
②根据几何概型的概率公式进行判断．
③根据排列组合的计数原理进行判断．
④根据正态分布的概率关系进行判断．

解答 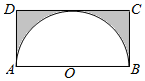解：①把函数y=3sin（2x+$\frac{π}{3}$）的图象向右平移$\frac{π}{6}$个单位，得到y=3sin[2（x-$\frac{π}{6}$）+$\frac{π}{3}$]=3sin（2x-$\frac{π}{3}$+$\frac{π}{3}$）=3sin2x，即可得到y=3sin2x的图象；故①正确，
解：已知如图所示：长方形面积为2，以O为圆心，1为半径作圆，在矩形内部的部分（半圆）面积为 $\frac{π}{2}$，
因此取到的点到O的距离大于1的概率P=$\frac{2-\frac{π}{2}}{2}$=1-$\frac{π}{4}$；故②错误；
③可分以下2种情况：（1）A类选修课选1门，B类选修课选2门，有C₃¹C₄²种不同的选法；
                （2）A类选修课选2门，B类选修课选1门，有C₃²C₄¹种不同的选法．
∴根据分类计数原理知不同的选法共有C₃¹C₄²+C₃²C₄¹=18+12=30种．故要求两类课程中各至少选一门，则不同的选法共有30种正确，故③正确，
④在某项测量中，测量结果ξ服从正态分布N（2，σ²）（σ＞0）．则正态曲线关于x=2对称，
若ξ在（-∞，1）内取值的概率为0.1，则ξ在[1，2]的概率P（1＜x＜2）=0.5-0．=4，
则在（2，3）内取值的概率P（2＜x＜3）=P（1＜x＜2）=0.4．故④正确，
故答案为：①③④

点评 本题主要考查命题的真假判断，涉及的知识点较多，综合性较强，但难度不是很大．