练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知a，b，c分别为△ABC内角A，B，C的对边，A=$\frac{π}{4}$，a=2，bcosC-ccosB=2$\sqrt{2}$，则∠B=$\frac{5π}{8}$．

    分析 根据正弦定理将边化角，利用三角函数的恒等变换化简得出B，C的关系，结合三角形的内角和解出B．

    解答 解：∵bcosC-ccosB=2$\sqrt{2}$，∴sinBcosC-sinCcosB=$\sqrt{2}$sinA．
    即sin（B-C）=1．∴B-C=$\frac{π}{2}$．
    ∵B+C=π-A=$\frac{3π}{4}$，
    ∴B=$\frac{5π}{8}$．
    故答案为：$\frac{5π}{8}$．

    点评 本题考查了正弦定理在解三角形中的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

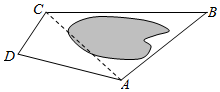    8．如图，为了测量A，C两点间的距离，选取同一平面上B、D两点，测出四边形ABCD各边的长度（单位：km）：AB=5，BC=8，CD=3，DA=5，且∠B与∠D互补，则AC的长为7km．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．在△ABC中，AB=3，AC=4，N是AB的中点，边AC（含端点）上存在点M，使得BM⊥CN，则cosA的取值范围为[$\frac{3}{8}$，1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知等差数列{an}的前n项和为Sn，若a1=1，a2=-1，则S4=（　　）
    A．6B．-6C．8D．-8

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．某班5位同学分别选择参加数学、物理、化学这3个学科的兴趣小组，每人限选一门学科，则每个兴趣小组都至少有1人参加的不同选择方法种数为（　　）
    A．150B．180C．240D．540

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

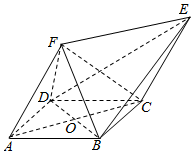    3．如图所示的几何体中，ABCD为菱形，ACEF为平行四边形，△BDF为等边三角形，O为AC与BD的交点．
    （Ⅰ）求证：BD⊥平面ACEF；
    （Ⅱ）若∠DAB=60°，AF=FC，求二面角B-EC-D的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．以下命题正确的是：①③④．
    ①把函数y=3sin（2x+$\frac{π}{3}$）的图象向右平移$\frac{π}{6}$个单位，可得到y=3sin2x的图象；
    ②四边形ABCD为长方形，AB=2，BC=1，O为AB中点，在长方形ABCD内随机取一点P，取得的P点到O的距离大于1的概率为1-$\frac{π}{2}$；
    ③某校开设A类选修课3门，B类选择课4门，一位同学从中共选3门，若要求两类课程中各至少选一门，则不同的选法共有30种；
    ④在某项测量中，测量结果ξ服从正态分布N（2，σ2）（σ＞0）．若ξ在（-∞，1）内取值的概率为0.1，则ξ在（2，3）内取值的概率为0.4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．下列命题中正确的是（　　）
    A．cosα≠0是α≠2kπ+$\frac{π}{2}$（k∈Z）的充分必要条件
    B．函数f（x）=3ln|x|的零点是（1，0）和（-1，0）
    C．设随机变量ξ服从正态分布N（0，1），若P（ξ＞1）=p，则P（-1＜ξ＜0）=$\frac{1}{2}$-p
    D．若将一组样本数据中的每个数据都加上同一个常数后，则样本的方差会改变

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知椭圆$\frac{x^2}{4}+\frac{y^2}{16}=1$被直线l截得弦的中点坐标为$（\frac{1}{2}，1）$，则直线l的方程2x+y-2=0．

    查看答案和解析>>

    同步练习册答案