
| A. | $({-\frac{3}{2},-1})$ | B. | $({-∞,-\frac{3}{2}}]∪[{-1,+∞})$ | C. | (-2,0) | D. | $({-∞,-\frac{3}{2}}]∪[{0,+∞})$ |
分析 本题研究的三个方程至少有一个有实根,此类题求解时通常转化为求其对立面,研究三个方程都没有实根时实数a的取值集合,其补集即是所求的实数a的取值范围
解答 解:不妨假设三个方程都没有实数根,则有$\left\{\begin{array}{l}{16{a}^{2}+16a-12<0}\\{(a-1)^{2}-4{a}^{2}<0}\\{4{a}^{2}+8a<0}\end{array}\right.$解得-$\frac{3}{2}$<a<-1
故三个方程x2+4ax-4a+3=0,x2+(a-1)x+a2=0,x2+2ax-2a=0至少有一个方程有实根时,实数a的取值范围为a≤-$\frac{3}{2}$或a≥-1
故选:B
点评 本题考查一元二次方程的根的分布与系数的关系,求解本题关键是理解题意“至少有一个方程有实根”,此题若从正面求解需要分的情况较多,不易解答,而对立面易求解,故采取了求三个方程都没有实数根时参数的取值范围,再求其补集得出答案,此解法应用了反证法的思想,其规律称为正难则反,解题是题设中出现了“至多”,“至少”这样的字样时,要注意使用本题这样的解法技巧.


科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<a<b | C. | b<c<a | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
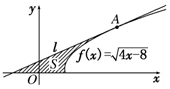 如图,过点A(6,4)作曲线f(x)=$\sqrt{4x-8}$的切线l.
如图,过点A(6,4)作曲线f(x)=$\sqrt{4x-8}$的切线l.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com