
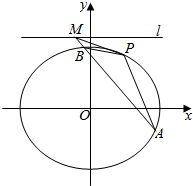
 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,3),离心率e=$\frac{1}{2}$,直线1的方程为y=4.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,3),离心率e=$\frac{1}{2}$,直线1的方程为y=4.分析 (Ⅰ)通过将点P(2,3)代入椭圆方程,结合离心率计算即得结论;
(Ⅱ)分AB斜率存在、不存在两种情况讨论,结合韦达定理计算即得结论.
解答 解:(Ⅰ)∵椭圆C经过点P(2,3),
∴$\frac{4}{{a}^{2}}$+$\frac{9}{{b}^{2}}$=1,
又∵e=$\frac{c}{a}$=$\frac{1}{2}$,a2=b2+c2,
∴a2=16,b2=12,
∴椭圆C的方程为:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$;
(Ⅱ)结论:存在常数λ=2,使得$\frac{1}{{k}_{1}}$十$\frac{1}{{k}_{2}}$=$\frac{2}{{k}_{3}}$.
理由如下:
①当AB斜率存在时,不妨设为y=kx+3,
联立直线AB与椭圆方程,消去y整理得:(3+4k2)x2+24kx-12=0,
设A(x1,y1),B(x2,y2),则x1+x2=-$\frac{24k}{3+4{k}^{2}}$,x1x2=$\frac{-12}{3+4{k}^{2}}$,
∴$\frac{1}{{k}_{1}}$十$\frac{1}{{k}_{2}}$=$\frac{{x}_{1}-2}{{y}_{1}-3}$+$\frac{{x}_{2}-2}{{y}_{2}-3}$
=$\frac{{x}_{1}-2}{k{x}_{1}}$+$\frac{{x}_{2}-2}{k{x}_{2}}$
=$\frac{1}{k}$[(1-$\frac{2}{{x}_{1}}$)+(1-$\frac{2}{{x}_{2}}$)]
=$\frac{2}{k}$(1-$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$)
=$\frac{2}{k}$(1-$\frac{-24k}{-12}$)
=$\frac{2}{k}$-4,
令y=4,则kx+3=4,从而M($\frac{1}{k}$,4),
则$\frac{λ}{{k}_{3}}$=λ•$\frac{2-\frac{1}{k}}{3-4}$=$\frac{λ}{k}$-2λ,
∵$\frac{1}{{k}_{1}}$十$\frac{1}{{k}_{2}}$=$\frac{λ}{{k}_{3}}$,
∴对比可知λ=2;
②当AB斜率不存在时,不妨设A(0,2$\sqrt{3}$),B(0,-2$\sqrt{3}$),M(0,4),
则$\frac{1}{{k}_{1}}$十$\frac{1}{{k}_{2}}$=$\frac{2-0}{3-2\sqrt{3}}$+$\frac{2-0}{3+2\sqrt{3}}$=-4,
$\frac{1}{{k}_{3}}$=-2,当λ=2时也成立;
综上所述,存在常数λ=2,使得$\frac{1}{{k}_{1}}$十$\frac{1}{{k}_{2}}$=$\frac{2}{{k}_{3}}$.
点评 本题考查椭圆的简单性质,考查运算求解能力,考查分类讨论的思想,注意解题方法的积累,属于中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
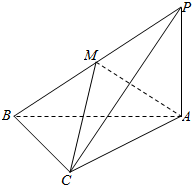 在三棱锥P-ABC中,∠PAB=∠PAC=∠ABC=90°,M是PB的中点,PA=AB=2.
在三棱锥P-ABC中,∠PAB=∠PAC=∠ABC=90°,M是PB的中点,PA=AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
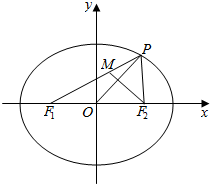 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1、F2,P是椭圆上一点,M在PF1上,且满足$\overrightarrow{{F_1}M}=λ\overrightarrow{MP}$(λ∈R),PO⊥F2M,O为坐标原点.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1、F2,P是椭圆上一点,M在PF1上,且满足$\overrightarrow{{F_1}M}=λ\overrightarrow{MP}$(λ∈R),PO⊥F2M,O为坐标原点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
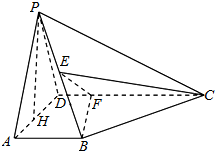 如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,E是PB的中点,F是CD上的点,PH为△PAD中AD边上的高.
如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,E是PB的中点,F是CD上的点,PH为△PAD中AD边上的高.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com