
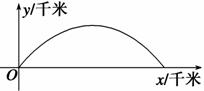
如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米,某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-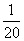 (1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1)求炮的最大射程.
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a不超过多少时,炮弹可以击中它?请说明理由.
 |
科目:高中数学 来源: 题型:
已知数列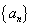 的前
的前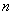 项和为
项和为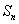
(1)若数列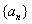 是等比数列,满足
是等比数列,满足 ,
, 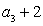 是
是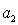 ,
,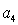 的等差
的等差 中项,求数列
中项,求数列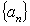 的通项公式;
的通项公式;
(2)是否存在等差数列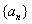 ,使对任意
,使对任意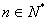 都有
都有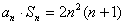 ?若存在,请求出所有满足条件的等差数列;若不存在,请说明理由.
?若存在,请求出所有满足条件的等差数列;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知定义域为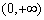 的函数
的函数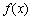 满足:对任意
满足:对任意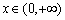 ,恒有
,恒有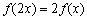 成立;当
成立;当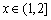 时,
时,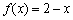 .给出如下结论:
.给出如下结论:
①对任意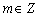 ,有
,有 ;
;
②函数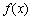 的值域为
的值域为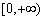 ;
;
③存在 ,使得
,使得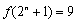 ;
;
④“函数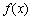 在区间
在区间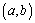 上单调递减”的充要条件是 “存在
上单调递减”的充要条件是 “存在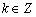 ,使得
,使得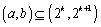 ”,
”,
其中所有正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
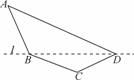
某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示,为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求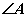 和
和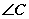 互补,且AB=BC
互补,且AB=BC
(1) 设AB=x米,cosA=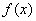 ,求
,求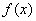 的解析式,并指出x的取值范围.
的解析式,并指出x的取值范围.
(2) 求四边形ABCD面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com