
| sinA |
| sinB |
| a |
| c |
| A、等边三角形 |
| B、等腰非等边三角形 |
| C、直角三角形 |
| D、钝角三角形 |
| sinA |
| sinB |
| a |
| c |
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
| π |
| 3 |
| a |
| sinA |
| b |
| sinB |
| sinA |
| sinB |
| a |
| b |
| sinA |
| sinB |
| a |
| c |
| a |
| b |
| a |
| c |


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
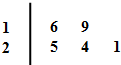 学校为了了解学生每个月在校期间参加体育锻炼的时间,从某班选取5名学生进行调查,他们参加体育锻炼的时间用茎叶图记录如图所示(单位:小时),则这组数据的中位数和方差分别是( )
学校为了了解学生每个月在校期间参加体育锻炼的时间,从某班选取5名学生进行调查,他们参加体育锻炼的时间用茎叶图记录如图所示(单位:小时),则这组数据的中位数和方差分别是( )| A、21和10.8 |
| B、24和10.8 |
| C、25和9.2 |
| D、5和9.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com