
分析 (1)根据曲线y=f(x)在P(1,y0)处的切线平行于直线y=-x+1,则f′(1)=-1,求出a,对函数求导,l利用导函数,在定义域中求出函数的单调区间.
(2)f′(x)=$\frac{-a}{{x}^{2}}+\frac{1}{x}=\frac{x-a}{{x}^{2}}$,分a≤0,a≥e,0<e<e讨论函数的最小值,建立有关a的方程,求出a即可.
解答 解:(1)函数f(x)的定义域为(0,+∞),
∵y=f(x)在点P(1,y0)处的切线平行于直线y=-x+1,
∴f′(1)=-1,f′(x)=$\frac{-a}{{x}^{2}}+\frac{1}{x}=\frac{x-a}{{x}^{2}}$,则f′(1)=1-a=-1,解得a=2,
此时f′(x)=$\frac{x-2}{{x}^{2}}$,
由f′(x)>0,解得x>2,此时函数单调递增,增区间为(2,+∞),
由f′(x)<0,解得0<x<2,此时函数单调递增,减区间为(0,2).
(2)f′(x)=$\frac{-a}{{x}^{2}}+\frac{1}{x}=\frac{x-a}{{x}^{2}}$,
1)当a≤0时,f′(x)≥0在(0,e]上恒成立,f(x)在(0,e]上递增,故不存在最小值.
2)当a≥e时,f′(x)≤0在(0,e]上恒成立,f(x)在(0,e]上递减,故存在最小值为f(e)=$\frac{a}{e}=1$,⇒a=e符合题意.
3)0<a<e时,f′(x)≥0在(a,e]上恒成立,f(x)在(a,e]上递增,f′(x)≤0在(0,a]上恒成立,f(x)在(0,a]上递减,
故存在最小值为f(a)=lna=1⇒a=e不符合题意.
综上,存在实数a=e,使函数y=f(x)在x∈(0,e]上有最小值1.
点评 本题考查函数的导数综合应用,解题的关键是根据参数的不同取值讨论函数的导函数的正负确定函数的单调区间,从而确定最小值,属于中档题.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:解答题
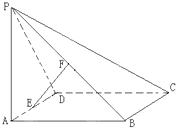 如图:四棱锥P-ABCD的底面是平行四边形,∠DAB=60°,平面PAB⊥ABD,
如图:四棱锥P-ABCD的底面是平行四边形,∠DAB=60°,平面PAB⊥ABD,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
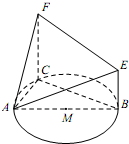 如图,某简单几何体的一个面ABC内接于圆M,AB是圆M的直径,CF∥BE,BE⊥平面ABC,且AB=2,AC=1,BE+CF=7.
如图,某简单几何体的一个面ABC内接于圆M,AB是圆M的直径,CF∥BE,BE⊥平面ABC,且AB=2,AC=1,BE+CF=7.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (0,-1) | C. | (-$\frac{1}{16}$,0) | D. | (0,-$\frac{1}{16}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 数学成绩好 | 数学成绩一般 | 总计 | |
| 物理成绩好 | |||
| 物理成绩一般 | |||
| 总计 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com