
分析 (1)根据幂函数的图象和性质,可得5${\;}^{\frac{3}{2}}$>2${\;}^{\frac{3}{2}}$>${1}^{\frac{3}{2}}$=1,根据指数函数的图象和性质,可判断${(\frac{1}{2})}^{3}$<${(\frac{1}{2})}^{0}$=1,进而得到答案.
(2)根据指数函数的图象和性质,可判断($\frac{3}{4}$)${\;}^{-\frac{1}{2}}$>($\frac{3}{4}$)${\;}^{-\frac{1}{3}}$>${(\frac{3}{4})}^{0}$=1,($\frac{3}{2}$)${\;}^{-\frac{2}{3}}$<($\frac{3}{2}$)0=1,进而得到答案.
解答 解:(1)∵y=${x}^{\frac{3}{2}}$在(0,+∞)上为增函数,故5${\;}^{\frac{3}{2}}$>2${\;}^{\frac{3}{2}}$>${1}^{\frac{3}{2}}$=1,
∵y=$(\frac{1}{2})^{x}$为减函数,故${(\frac{1}{2})}^{3}$<${(\frac{1}{2})}^{0}$=1,
故5${\;}^{\frac{3}{2}}$>2${\;}^{\frac{3}{2}}$>${(\frac{1}{2})}^{3}$;
(2)∵y=${(\frac{3}{4})}^{x}$为减函数,故($\frac{3}{4}$)${\;}^{-\frac{1}{2}}$>($\frac{3}{4}$)${\;}^{-\frac{1}{3}}$>${(\frac{3}{4})}^{0}$=1,
∵y=${(\frac{3}{2})}^{x}$为增函数,故($\frac{3}{2}$)${\;}^{-\frac{2}{3}}$<($\frac{3}{2}$)0=1,
故($\frac{3}{4}$)${\;}^{-\frac{1}{2}}$>($\frac{3}{4}$)${\;}^{-\frac{1}{3}}$>($\frac{3}{2}$)${\;}^{-\frac{2}{3}}$.
点评 本题考查的知识点是数的大小比较,熟练掌握相应指数函数和幂函数的单调情是解答的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
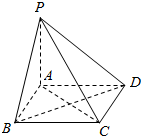 如图所示,四边形ABCD为正方形,PA⊥平面ABCD,则在平面PAB,平面PAD,平面PCD,平面PBC及平面ABCD中,互相垂直的有( )
如图所示,四边形ABCD为正方形,PA⊥平面ABCD,则在平面PAB,平面PAD,平面PCD,平面PBC及平面ABCD中,互相垂直的有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com