
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 过坐标原点
过坐标原点![]() 且圆心在曲线
且圆心在曲线![]() 上.
上.
(1)若圆![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() (不同于原点
(不同于原点![]() ),求证:
),求证:![]() 的面积为定值;
的面积为定值;
(2)设直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,且
,且![]() ,求圆
,求圆![]() 的方程;
的方程;
(3)点![]() 在直线
在直线![]() 上,过点
上,过点![]() 引圆
引圆![]() (题(2))的两条切线
(题(2))的两条切线![]() ,切点为
,切点为![]() ,求证:直线
,求证:直线![]() 恒过定点.
恒过定点.
【答案】(1)证明见详解
(2)![]()
(3)证明见详解
【解析】
(1)设出圆![]() 的圆心,写出圆
的圆心,写出圆![]() 的标准方程,求出
的标准方程,求出![]() 两点,再计算
两点,再计算![]() 的面积。
的面积。
(2)由题意知![]() 为
为![]() 的中垂线,即可得到直线
的中垂线,即可得到直线![]() ,即可求出圆心
,即可求出圆心![]() 。
。
(3)设出点![]() ,写出以点
,写出以点![]() 为圆心切线长为半径的圆的方程,利用圆
为圆心切线长为半径的圆的方程,利用圆![]() -圆
-圆![]() ,即可求出直线
,即可求出直线![]() 的方程,再说明其过定点。
的方程,再说明其过定点。
(1)证明:设圆![]() 的圆心为
的圆心为![]() ,则半径
,则半径![]() ,
,
所以圆![]() 的标准方程为
的标准方程为![]() ,
,
则![]() 、
、![]() ,
,
所以![]() 的面积
的面积![]()
所以![]() 的面积为定值
的面积为定值![]() 。
。
(2)因为![]() ,即O在线段
,即O在线段![]() 的中垂线上,又圆心
的中垂线上,又圆心![]() 在线段
在线段![]() 的中垂线上,
的中垂线上,
所以![]() 为
为![]() 的中垂线,又
的中垂线,又![]()
所以![]() ,直线
,直线![]() 为
为![]() ,联立
,联立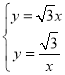 解得
解得![]() ,
,![]() 舍
舍
所以![]() ,
,
即圆![]() 的标准方程为
的标准方程为![]()
(3)证明:设点![]() ,则圆心
,则圆心![]() 到点
到点![]() 的距离
的距离![]()
切线长![]() ,
,
即以点![]() 为圆心,切线长为半径的圆为
为圆心,切线长为半径的圆为![]()
则圆![]() 与圆
与圆![]() 的相交弦直线
的相交弦直线![]() 为
为![]()
化简得![]()
即![]() 过定点
过定点![]()


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,
,![]() 是
是![]() 上任意一点。
上任意一点。

(1)求证:![]() ;
;
(2)当![]() 面积的最小值是9时,在线段
面积的最小值是9时,在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 与平面
与平面![]() 所成角的正切值为2?若存在?求出
所成角的正切值为2?若存在?求出![]() 的值,若不存在,请说明理由
的值,若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 个不全相等的正数
个不全相等的正数![]() ,
,![]() ,…,
,…,![]() 依次围成一个圆圈.
依次围成一个圆圈.
(Ⅰ)设![]() ,且
,且![]() ,
,![]() ,
,![]() ,…,
,…,![]() 是公差为
是公差为![]() 的等差数列,而
的等差数列,而![]() ,
,![]() ,
,![]() ,…,
,…,![]() 是公比为
是公比为![]() 的等比数列,数列
的等比数列,数列![]() ,
,![]() ,…,
,…,![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,
,![]() ,若数列
,若数列![]() ,
,![]() ,…,
,…,![]() 每项是其左右相邻两数平方的等比中项,求
每项是其左右相邻两数平方的等比中项,求![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,![]() ,求符合条件的
,求符合条件的![]() 的个数.
的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司利用![]() 线上、实体店线下销售产品
线上、实体店线下销售产品![]() ,产品
,产品![]() 在上市
在上市![]() 天内全部售完.据统计,线上日销售量
天内全部售完.据统计,线上日销售量![]() 、线下日销售量
、线下日销售量![]() (单位:件)与上市时间
(单位:件)与上市时间![]()
![]() 天的关系满足:
天的关系满足:![]()
![]()
![]() ,产品
,产品![]() 每件的销售利润为
每件的销售利润为![]() (单位:元)(日销售量
(单位:元)(日销售量![]() 线上日销售量
线上日销售量![]() 线下日销售量).
线下日销售量).
(1)设该公司产品![]() 的日销售利润为
的日销售利润为![]() ,写出
,写出![]() 的函数解析式;
的函数解析式;
(2)产品![]() 上市的哪几天给该公司带来的日销售利润不低于
上市的哪几天给该公司带来的日销售利润不低于![]() 元?
元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村电费收取有以下两种方案供农户选择:方案一:每户每月收管理费2元,月用电不超过30度时,每度0.5元;超过30度时,超过部分按每度0.6元收取. 方案二:不收管理费,每度0.58元.
(1)求方案一收费![]() 元与用电量x (度)之间的函数关系;
元与用电量x (度)之间的函数关系;
(2)老王家九月份按方案一交费35元,问老王家该月用电多少度?
(3)老王家月用电最在什么范围时,选择方案一比选择方案二更好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用符号“![]() ”或“
”或“![]() ”填空:
”填空:
(1)设A为所有亚洲国家组成的集合,则中国______________A,美国__________A,印度____________A,英国_____________A;
(2)若![]() ,则-1_____________A;
,则-1_____________A;
(3)若![]() ,则3________________B;
,则3________________B;
(4)若![]() ,则8_______________C,9.1____________C.
,则8_______________C,9.1____________C.
查看答案和解析>>
科目:高中数学 来源: 题型:
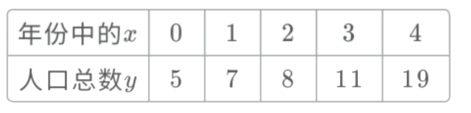
【题目】某城市理论预测2014年到2018年人口总数![]() (单位:十万)与年份(用
(单位:十万)与年份(用![]() 表示)的关系如表所示:
表示)的关系如表所示:
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(3)据此估计2019年该城市人口总数.
(参考数据: ![]()
![]() )
)
参考公式:线性回归方程为![]() ,其中
,其中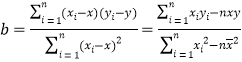 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右顶点为A,上顶点为B.已知椭圆的离心率为
的右顶点为A,上顶点为B.已知椭圆的离心率为![]() ,
,![]() .
.
(1)求椭圆的方程;
(2)设直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,
两点,![]() 与直线
与直线![]() 交于点M,且点P,M均在第四象限.若
交于点M,且点P,M均在第四象限.若![]() 的面积是
的面积是![]() 面积的2倍,求
面积的2倍,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com