
分析 由$\frac{(k+1)^{2}}{2015}$-$\frac{{k}^{2}}{2015}$=$\frac{2k+1}{2015}$,把1≤k≤2016,k∈N分为两类,当k=0,1,2,3,…,1007时,求出满足条件的[$\frac{{k}^{2}}{2015}$]的个数为503,当k=1008,1009,…,2016时,求出满足条件的[$\frac{{k}^{2}}{2015}$]的个数为1009,则答案可求.
解答 解:∵当k=0,1,2,3,…,1007时,
$\frac{(k+1)^{2}}{2015}-\frac{{k}^{2}}{2015}=\frac{2k+1}{2015}≤1$,
∴[$\frac{(k+1)^{2}}{2015}$]=[$\frac{{k}^{2}}{2015}$],或[$\frac{(k+1)^{2}}{2015}$]=[$\frac{{k}^{2}}{2015}$]+1,
∵[$\frac{100{7}^{2}}{2015}$]=503,[$\frac{{1}^{2}}{2015}$]=0,
∴当k=0,1,2,3,…,1007时,[$\frac{{k}^{2}}{2015}$]能取0,1,2,3,…,503共504个数,
又当k=1008,1009,…,2016时,
$\frac{(k+1)^{2}}{2015}$-$\frac{{k}^{2}}{2015}$=$\frac{2k+1}{2015}>1$,
∴[$\frac{(k+1)^{2}}{2015}$]≥[$\frac{{k}^{2}}{2015}$]+1,
即[$\frac{100{8}^{2}}{2015}$],[$\frac{100{9}^{2}}{2015}$],…,[$\frac{201{6}^{2}}{2015}$]共有2016-1007=1009个不同的数.
∵[$\frac{100{8}^{2}}{2015}$]=504>503=[$\frac{100{7}^{2}}{2015}$].
∴A中元素的个数是1009+503=1512.
故答案为:1512.
点评 本题考查元素与集合间关系的判断,注意对[x]定义的理解,借助于$\frac{(k+1)^{2}}{2015}$-$\frac{{k}^{2}}{2015}$=$\frac{2k+1}{2015}$分类求解,使繁杂的问题变得相对简单,该题是中档题.


科目:高中数学 来源: 题型:解答题
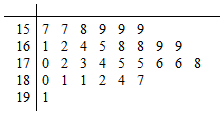 为了解某种树苗培育情况,研究所在苗圃基地花木园中随机抽出30株树苗的主体高,编成如图所示的茎叶图,若苗主体高在169cm以上(包括169cm)定义为“优质苗”,高在169cm以下(不包括169cm)定义为“普苗”
为了解某种树苗培育情况,研究所在苗圃基地花木园中随机抽出30株树苗的主体高,编成如图所示的茎叶图,若苗主体高在169cm以上(包括169cm)定义为“优质苗”,高在169cm以下(不包括169cm)定义为“普苗”查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
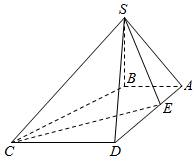 如图,在四棱锥S-ABCD中,SB⊥底面ABCD,底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是( )
如图,在四棱锥S-ABCD中,SB⊥底面ABCD,底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com