
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 利用基本不等式求出$\frac{12}{t+\frac{1}{t}}$在t∈(0,+∞)上的最大值,得到a的范围;再利用数形结合求得直线x-2y+a=0与曲线y-1=$\sqrt{4+2x-{x}^{2}}$有2个公共点的a的范围,然后结合必要条件、充分条件及充要条件的判断方法得答案.
解答 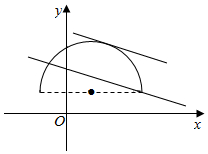 解:对于p,∵t∈(0,+∞),
解:对于p,∵t∈(0,+∞),
∴$t+\frac{1}{t}≥2$(当且仅当t=1时取“=”),则$\frac{12}{t+\frac{1}{t}}≤6$,
∴a≥6;
对于q,
由曲线y-1=$\sqrt{4+2x-{x}^{2}}$,得(x-1)2+(y-1)2=5($1-\sqrt{5}≤x≤1+\sqrt{5}$,y≥1),
如图,当直线x-2y+a=0过(1+$\sqrt{5}$,1)时,有1+$\sqrt{5}-2$+a=0,a=1-$\sqrt{5}$,
由(1,1)到直线x-2y+a=0的距离为d=$\frac{|1-2+a|}{\sqrt{5}}=\sqrt{5}$,解得a=-4或a=6,
∴要使直线x-2y+a=0与曲线y-1=$\sqrt{4+2x-{x}^{2}}$有2个公共点,
则1-$\sqrt{5}<a<6$.
若¬p成立,则a<6,不一定又q成立,反之,若q成立,即1-$\sqrt{5}<a<6$,一定有¬p成立.
则¬p是q的必要不充分条件.
故选:A.
点评 本题考查必要条件、充分条件及充要条件的判断方法,考查了恒成立问题的求法,体现了数形结合的解题思想方法,属中档题.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:解答题
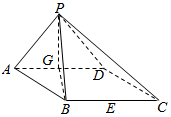 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,G为AD边的中点,E为BC所在直线上的一点
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,G为AD边的中点,E为BC所在直线上的一点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1840 | B. | 1860 | C. | 1880 | D. | 2010 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com