
分析 (1)直接由题意列式可得d与q的函数关系式;
(2)(Ⅰ)由等比数列的通项公式得答案;
(Ⅱ)求出数列{an}的通项公式,把数列{an}、{bn}的通项公式代入cn=$\frac{{n}^{2}}{{a}_{n}{b}_{n}+1}$,放缩后利用错误相减法证明.
解答 (1)解:由a1=1,a1+a3=b2,2a22=b3,
得1+1+2d=b1q,$2(1+d)^{2}={b}_{1}{q}^{2}$,联立得2(1+d)2=2(1+d)q,
得1+d=q;
(2)当d=3,且b1=2时,q=4,b1=2,
(Ⅰ)解:由等比数列的通项公式可得${b}_{n}=2•{4}^{n-1}={2}^{2n-1}$;
(Ⅱ)证明:an=1+3(n-1)=3n-2,
cn=$\frac{{n}^{2}}{{a}_{n}{b}_{n}+1}$=$\frac{{n}^{2}}{2(3n-2)•{4}^{n-1}+1}$=$\frac{{n}^{2}}{(\frac{3}{2}n-1)•{4}^{n}+1}$>$\frac{{n}^{2}}{(\frac{3}{2}n-1)•{4}^{n}+{4}^{n}}$=$\frac{{n}^{2}}{\frac{3}{2}n•{4}^{n}}$=$\frac{2}{3}n•\frac{1}{{4}^{n}}$.
∴${T}_{n}=\frac{2}{3}(1•\frac{1}{4}+2•\frac{1}{{4}^{2}}+…+n•\frac{1}{{4}^{n}})$,①
令${R}_{n}=1•\frac{1}{4}+2•\frac{1}{{4}^{2}}+…+n•\frac{1}{{4}^{n}}$,得:
$\frac{1}{4}{R}_{n}=1•\frac{1}{{4}^{2}}+2•\frac{1}{{4}^{3}}+…+n•\frac{1}{{4}^{n+1}}$,
两式作差得:$\frac{3}{4}{R}_{n}=\frac{1}{4}+\frac{1}{{4}^{2}}+…+\frac{1}{{4}^{n}}-n•\frac{1}{{4}^{n+1}}$=$\frac{\frac{1}{4}(1-\frac{1}{{4}^{n}})}{1-\frac{1}{4}}-n•\frac{1}{{4}^{n+1}}=\frac{1}{3}(1-\frac{1}{{4}^{n}})-n•\frac{1}{{4}^{n+1}}$,
∴${R}_{n}=\frac{4}{9}(1-\frac{1}{{4}^{n}})-\frac{n}{9}•\frac{1}{{4}^{n}}$,代入①,得${T}_{n}=\frac{8}{27}(1-\frac{1}{{4}^{n}})-\frac{2n}{27}•\frac{1}{{4}^{n}}$>$\frac{8}{27}$.
点评 本题是等差数列和等比数列的综合题,考查了等差数列和等比数列的通项公式,训练了错位相减法求数列的和,训练了放缩法证明数列不等式,是中档题.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:选择题
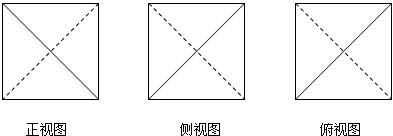
| A. | 3 | B. | 6 | C. | 3+$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
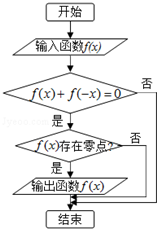 某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )
某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )| A. | f(x)=lg$\frac{x-1}{x+1}$ | B. | f(x)=ex | C. | f(x)=$\frac{1}{{x}^{3}}$ | D. | f(x)=ex-e-x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{π}{2}$ | C. | 1 | D. | π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com