
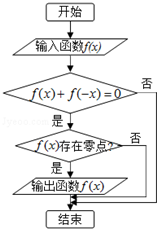
 某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )
某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )| A. | f(x)=lg$\frac{x-1}{x+1}$ | B. | f(x)=ex | C. | f(x)=$\frac{1}{{x}^{3}}$ | D. | f(x)=ex-e-x |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是输出满足条件①f(x)+f(-x)=0,即函数f(x)为奇函数②f(x)存在零点,即函数图象与x轴有交点.逐一分析四个答案中给出的函数的性质,不难得到正确答案.
解答 解:∵A:f(x)=lg$\frac{x-1}{x+1}$的函数图象与x轴没有交点,故不满足条件②
B:f(x)=ex,不是奇函数,故不满足条件①
又∵C:f(x)=$\frac{1}{{x}^{3}}$的函数图象与x轴没有交点,故不满足条件②
而D:f(x)=ex-e-x既是奇函数,而且函数图象与x也有交点,符合输出的条件.
故选:D.
点评 根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是:①分析流程图(或伪代码),从流程图(或伪代码)中即要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模,本题属于基础题.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:解答题
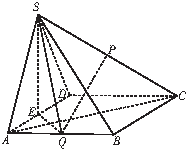 如图,在棱锥S-ABCD中,底面ABCD为菱形,平面SAD⊥平面ABCD,SA=SD,E、P、Q分别是棱AD、SC、AB的中点.
如图,在棱锥S-ABCD中,底面ABCD为菱形,平面SAD⊥平面ABCD,SA=SD,E、P、Q分别是棱AD、SC、AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{a}$) | B. | ($\frac{1}{a}$,+∞) | C. | (-∞,$\frac{1}{a}$) | D. | (-∞,a) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1) | B. | (-1,2) | C. | (-∞,-1)∪(2,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x=0,则x2-x=0”的逆否命题为真命题 | |
| B. | 若命题P:?n∈N,n2>2n,则¬P:?n∈N,n2≤2n | |
| C. | 若“p∧q”为假命题,则“p∨q”为真命题 | |
| D. | 命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0或n=0” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com