
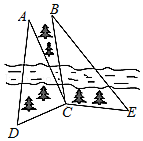
 如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据;
如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据;分析 (1)利用周角定义求出∠DCE度数,再由CD与CE的长,利用三角形面积公式求出三角形CDE面积即可;
(2)连接AB,在直角三角形ACD中,利用锐角三角函数定义求出AC的长,在直角三角形BCE中,求出∠CBE度数,利用正弦定理求出BC的长,在三角形ABC中,利用余弦定理求出AB的平方即可.
解答 解:(1)在△CDE中,∠DCE=360°-90°-30°-105°=135°,
∴S△CDE=$\frac{1}{2}$CD•CE•sin135°=$\frac{1}{2}$×2×2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$(平方百米);
(2)连接AB,
根据题意知,在Rt△ACD中,AC=DC•tan∠ADC=2×tan60°=2$\sqrt{3}$(百米),
在△BCE中,∠CBE=180°-∠BCE-∠CEB=180°-105°-45°=30°,
由正弦定理得$\frac{BC}{sin∠CEB}$=$\frac{CE}{sin∠CBE}$,代入求得BC=2$\sqrt{2}$(百米),
在△ABC中,由余弦定理得:AB2=AC2+BC2-2AC•BCcos∠ACB,
则AB2=12+8-2×2$\sqrt{3}$×2$\sqrt{2}$•$\frac{\sqrt{3}}{2}$=20-12$\sqrt{2}$,
∴AB=2$\sqrt{5-3\sqrt{2}}$.
点评 此题考查了正弦、余弦定理,三角形面积公式,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,0) | B. | (-∞,-2) | C. | (-8,0) | D. | (0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p是假命题,其否定是:?k∈(2,+∞),直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1有交点 | |
| B. | p是真命题,其否定是:?k∈(0,2),直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1无交点 | |
| C. | p是假命题,其否定是:?k∈(0,2),直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1无交点 | |
| D. | p是真命题,其否定是:?k∈(2,+∞),直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1无交点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com