
分析 先假设存在这样的直线l,分类讨论:斜率存在和斜率不存在设出直线l的方程,①当k存在时,与双曲线方程联立,消去y,得到关于x的一元二次方程,通过△=(2k2-2k)2-4(2-k2)(-k2+2k-3)>0,可求k的范围,再由A是线段PQ的中点,则 $\frac{{x}_{1}+{x}_{2}}{2}$=1,可求k,看是否矛盾,②当k不存在时,直线经过点B但不满足条件,故符合条件的直线l不存在,综合可求.
解答 解:设过点B(1,1)的直线方程为y=k(x-1)+1(当k存在时)或x=1(当k不存在时).
①当k存在时,有$\left\{\begin{array}{l}{y=k(x-1)+1}\\{{x}^{2}-\frac{{y}^{2}}{2}=1}\end{array}\right.$,得(2-k2)x2+(2k2-2k)x-k2+2k-3=0 (1)
当直线与双曲线相交于两个不同点,则必有△=(2k2-2k)2-4(2-k2)(-k2+2k-3)>0,
∴k<$\frac{3}{2}$
设P(x1,y1),Q(x2,y2)
∴x1+x2=$\frac{2(k-{k}^{2})}{2-{k}^{2}}$,又A(1,1)为线段PQ的中点
∴$\frac{{x}_{1}+{x}_{2}}{2}$=1,即$\frac{2(k-{k}^{2})}{2-{k}^{2}}$=1
∴k=2
当k=2,使2-k2≠0但使△<0
因此当k=2时,方程(1)无实数解
故过点A(1,1)与双曲线交于两点P、Q且B为线段PQ中点的直线不存在.
②当k不存在时,即当x=1时,直线经过点B,但不满足条件,
综上,符合条件的直线l不存在.
点评 本题考察了直线与双曲线的位置关系,特别是相交时的中点弦问题,方程的根与系数关系的应用,及利用方程思想判断直线与曲线位置关系.


科目:高中数学 来源: 题型:填空题
 如图,是某铁路客运部门设计的甲、乙两地之间旅客托运行李的费用c(单位:元)与行李重量w(单位:千克)之间的流程图.假定某旅客的托运费为10元,则该旅客托运的行李重量为20千克.
如图,是某铁路客运部门设计的甲、乙两地之间旅客托运行李的费用c(单位:元)与行李重量w(单位:千克)之间的流程图.假定某旅客的托运费为10元,则该旅客托运的行李重量为20千克.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 36 | C. | 48 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
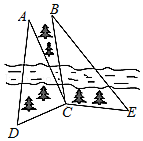 如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据;
如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{20}$=1 | B. | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{80}$=1 | D. | $\frac{{x}^{2}}{80}$-$\frac{{y}^{2}}{20}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com