
分析 由f(x)是奇函数得到f(-x)=-f(x),由此可以得到|x+a|+|a-x|=2a>0,所以a得范围是(0,+∞).
解答 解:∵f(x)=$\frac{\sqrt{{a}^{2}-{x}^{2}}}{|x+a|-a}$是奇函数,
∴f(-x)=-f(x),即$\frac{\sqrt{{a}^{2}-{x}^{2}}}{|a-x|-a}$=-$\frac{\sqrt{{a}^{2}-{x}^{2}}}{|x+a|-a}$,
∴|x+a|-a=a-|a-x|,
∴|x+a|+|a-x|=2a>0,
∴a>0,
故答案为:(0,+∞).
点评 本题考查由f(x)是奇函数得到f(-x)=-f(x),由此可以得到|x+a|+|a-x|=2a>0,所以a得范围是(0,+∞).


科目:高中数学 来源: 题型:解答题
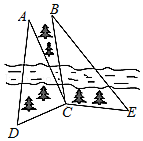 如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据;
如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
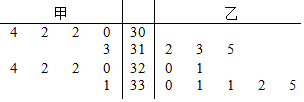
| A. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,s甲>s乙 | B. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,s甲<s乙 | ||
| C. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,s甲>s乙 | D. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,s甲<s乙 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
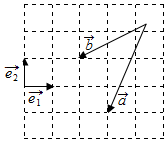 如图,设$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$为互相垂直的单位向量,则向量$\overrightarrow{a}$-$\overrightarrow{b}$可表示为( )
如图,设$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$为互相垂直的单位向量,则向量$\overrightarrow{a}$-$\overrightarrow{b}$可表示为( )| A. | 2$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$ | B. | 3$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$ | C. | 2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$ | D. | $\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{100}{101}$ | B. | $\frac{200}{101}$ | C. | $\frac{99}{100}$ | D. | $\frac{198}{100}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com