
| A. | p是假命题,其否定是:?k∈(2,+∞),直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1有交点 | |
| B. | p是真命题,其否定是:?k∈(0,2),直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1无交点 | |
| C. | p是假命题,其否定是:?k∈(0,2),直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1无交点 | |
| D. | p是真命题,其否定是:?k∈(2,+∞),直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1无交点 |
分析 求得双曲线的渐近线方程和斜率,由题意可得k>$\frac{3}{2}$或k<-$\frac{3}{2}$.可得命题P为真命题,运用命题的否定形式,即可得到结论.
解答 解:若直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1有交点,
由双曲线的渐近线方程y=±$\frac{3}{2}$x,
且双曲线的焦点在y轴上,
可得k>$\frac{3}{2}$或k<-$\frac{3}{2}$.
故?k∈(0,2),直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1有交点为真命题;
否定是:?k∈(0,2),直线y=kx与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1无交点.
故选:B.
点评 本题考查直线与双曲线的位置关系的判断,注意运用渐近线的斜率,考查运算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
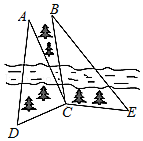 如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据;
如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
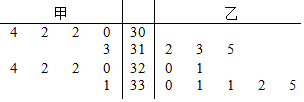
| A. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,s甲>s乙 | B. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,s甲<s乙 | ||
| C. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,s甲>s乙 | D. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,s甲<s乙 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
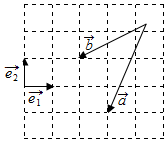 如图,设$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$为互相垂直的单位向量,则向量$\overrightarrow{a}$-$\overrightarrow{b}$可表示为( )
如图,设$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$为互相垂直的单位向量,则向量$\overrightarrow{a}$-$\overrightarrow{b}$可表示为( )| A. | 2$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$ | B. | 3$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$ | C. | 2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$ | D. | $\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com