
分析 将直线方程,代入椭圆方程,利用韦达定理及抛物线的性质求得$\frac{1}{丨AF丨}$+$\frac{1}{丨BF丨}$=1,利用基本不等式的性质,即可求得|AF|+2•|BF|的最小值.
解答 解:抛物线C:y2=4x的焦点F坐标(1,0),准线方程为x=-1.
设过F点的直线方程为y=k(x-1),设A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{y=k(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,化简后为:k2x2-(2k2+4)x+k2=0.
则x1+x2=$\frac{2{k}^{2}+4}{{k}^{2}}$,x1x2=1,
根据抛物线性质可知,|AF|=x1+1,|BF|=x2+1
∴$\frac{1}{丨AF丨}$+$\frac{1}{丨BF丨}$=$\frac{{x}_{1}+1+{x}_{2}+1}{({x}_{1}+1)({x}_{2}+1)}$=$\frac{{x}_{1}+{x}_{2}+2}{{x}_{1}+{x}_{2}+{x}_{1}{x}_{2}+1}$=1,
∴$\frac{1}{{|{AF}|}}+\frac{1}{{|{BF}|}}=\frac{2}{p}=1$,
|AF|+2•|BF|=$({|{AF}|+2•|{BF}|})•({\frac{1}{{|{AF}|}}+\frac{1}{{|{BF}|}}})$=$3+2•\frac{{|{BF}|}}{{|{AF}|}}+\frac{{|{AF}|}}{{|{BF}|}}≥3+2\sqrt{2}$.
当且仅当$\frac{2丨BF丨}{丨AF丨}$=$\frac{丨AF丨}{丨BF丨}$时,即丨AF丨=1+$\sqrt{2}$,丨BF丨=$\frac{\sqrt{2}(1+\sqrt{2})}{2}$时,取等号,
∴|AF|+2•|BF|的最小值3+2$\sqrt{2}$,
故答案为:3+2$\sqrt{2}$.
点评 本题考查直线与抛物线的位置关系,考查韦达定理,抛物线的性质以及基本不等式的性质,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
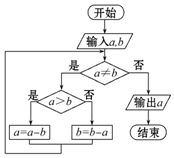 某同学根据“更相减损术”设计出程序框图(图).若输入a的值为98,b的值为63,则执行该程序框图输出的结果为( )
某同学根据“更相减损术”设计出程序框图(图).若输入a的值为98,b的值为63,则执行该程序框图输出的结果为( )| A. | 0 | B. | 7 | C. | 14 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com