
 2016��ijʡ�������Ƴ�15��ĸ��ʩ������������ҵ��λ�������ϱ����ƶȸĸ����������ҵ��λ���ʱ���ȫʡ�����»��ؽ���ְ����ְ�������ƶȣ�ij��Ϊ���˽�����������Щ�ĸ��ʩ��̬�ȣ��ڸ��������ȡ��50��������е��飬���������������루��λ����Ԫ����Χ��[15��75]����Ƶ�ʷֲ�ֱ��ͼ��ͬʱ�õ����и������������������Ը��������ɵ�����ͳ�Ʊ���
2016��ijʡ�������Ƴ�15��ĸ��ʩ������������ҵ��λ�������ϱ����ƶȸĸ����������ҵ��λ���ʱ���ȫʡ�����»��ؽ���ְ����ְ�������ƶȣ�ij��Ϊ���˽�����������Щ�ĸ��ʩ��̬�ȣ��ڸ��������ȡ��50��������е��飬���������������루��λ����Ԫ����Χ��[15��75]����Ƶ�ʷֲ�ֱ��ͼ��ͬʱ�õ����и������������������Ը��������ɵ�����ͳ�Ʊ���| ������ | ������ |
| [15��25�� | 4 |
| [25��35�� | 8 |
| [35��45�� | 12 |
| [45��55�� | 5 |
| [55��65�� | 2 |
| [65��75] | 2 |
���� ��1������Ƶ�ʺ�Ϊ1������Ƶ��ֱ��ͼ�Ļ�������ȫ���ɣ�
��2������ƽ�����Ķ��壬���ƽ���������������������弴�ɣ�
��3�����ݹŵ�����ʹ�ʽ���ֱ��оٳ����еĻ����¼������ҵ����������Ļ����¼����������ֵ��
��� �⣺��1���������ڰ�Ԫ�ڵ�Ƶ��Ϊ
1-0.01��10��3-0.02��10��2=0.3��
��$\frac{0.3}{10}$=0.03����ȫ���Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��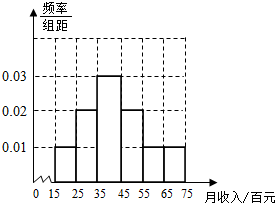
��2����Ƶ�ʷֲ�ֱ��ͼ������ƽ����Ϊ
20��0.1+30��0.2+40��0.3+50��0.2+60��0.1+70��0.1=43����Ԫ����
����50�˵�ƽ�����������Ϊ4300Ԫ��
��3��[35��45���ڵ�����Ϊ15�ˣ�����12���ɣ�3�˲��ɣ�
�Dz��ɵ���Ϊa��b��c������
[65��75]�ڵ�����Ϊ5�ˣ�����2���ɣ�3�˲��ɣ�
�Dz��ɵ�3��Ϊx��y��z��
�Ӳ��ɵ�6������ȡ2�ˣ������¼��ǣ�
ab��ac��ax��ay��az��bc��bx��by��bz��cx��cy��cz��xy��xz��yz��15�������
��������������������1000Ԫ����ab��ac��bc��xy��xz��yz����6�������
����������������벻����1000Ԫ�ĸ�����P=$\frac{6}{15}$=$\frac{2}{5}$��
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ�ŵ���ʵ����⣬���ڻ�����


 ���ݼ���ϵ�д�
���ݼ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|1��x��3} | B�� | {x|x��3} | C�� | {x|x��-1} | D�� | {x|-1��x��1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -10 | B�� | -5 | C�� | 5 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{3}{2}$ | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com