
分析 可作图:延长AB到E,使AE=2AB,连接CE,取CE中点F,连接AF,从而可得到$2\overrightarrow{AF}=3\overrightarrow{AD}$,从而求出DF=1,连接BF,这样便可说明点D在边BC上,并求出BC=6.取AB的中点M,连接DM,则有DM⊥AB,根据tanB=2便可求出AB=$\frac{4}{\sqrt{5}}$,过A作AN⊥BC,垂足为N,同理可求出$AN=\frac{8}{5}$,这样根据三角形的面积公式即可求出△ABC的面积.
解答 解:如图,延长AB到E,使AE=2AB,连接CE,取CE中点F,连接AF,则:
2$\overrightarrow{AF}=2\overrightarrow{AB}+\overrightarrow{AC}$;
即$2\overrightarrow{AF}=3\overrightarrow{AD}$;
∴$|\overrightarrow{AF}|=\frac{3}{2}|\overrightarrow{AD}|=3$;
∴$|\overrightarrow{DF}|=1$;
即$\frac{DF}{AD}=\frac{1}{2}$,连接BF,则:BF∥AC,且$\frac{BF}{AC}=\frac{1}{2}$;
∴点D在边BC上,且$\frac{BD}{CD}=\frac{1}{2},BD=2$,∴CD=4,∴BC=6;
取AB中点M,连接DM,则DM⊥AB;
设BM=x,∵tanB=2,∴DM=2x;
∴x2+(2x)2=4;
∴$x=\frac{2}{\sqrt{5}}$;
∴$AB=\frac{4}{\sqrt{5}}$,同理,过A作AN⊥BC,垂足为N,则:$B{N}^{2}+(2BN)^{2}=\frac{16}{5}$;
∴$BN=\frac{4}{5}$;
∴$AN=\frac{8}{5}$;
∴${S}_{△ABC}=\frac{1}{2}×6×\frac{8}{5}=\frac{24}{5}$.
故答案为:$\frac{24}{5}$.
点评 考查向量数乘的几何意义,向量加法的平行四边形法则,三角形中位线的性质,以及相似三角形对应边的比例关系,正切函数的定义,直角三角形边的关系,三角形的面积公式.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | -3 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}i$ | B. | $\frac{1}{2}i$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | -1 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
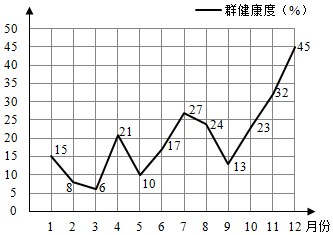 目前很多朋友都加入了微信群,大多数群成员认为有思想的群不仅仅是群里的人转发与主题有关的网页文章,而且群成员之间还有文字或语音的交流,因此规定$\frac{网页类型分享}{文字语音聊天}$为“群健康度”,为此群主统计了一年的群里聊天记录(假定该群进群由群主同意邀请,且无插入广告),并将聊天记录中的网页类型分享和文字语音聊天内容进行了分类统计,并按照“群健康度”制作了分析趋势图,假定“群健康度”小于20%为群氛围优良,“群健康度”大于30%为群氛围不合理.
目前很多朋友都加入了微信群,大多数群成员认为有思想的群不仅仅是群里的人转发与主题有关的网页文章,而且群成员之间还有文字或语音的交流,因此规定$\frac{网页类型分享}{文字语音聊天}$为“群健康度”,为此群主统计了一年的群里聊天记录(假定该群进群由群主同意邀请,且无插入广告),并将聊天记录中的网页类型分享和文字语音聊天内容进行了分类统计,并按照“群健康度”制作了分析趋势图,假定“群健康度”小于20%为群氛围优良,“群健康度”大于30%为群氛围不合理.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com