
| A. | [-1,$\frac{1}{2}$) | B. | [-1,1] | C. | ($\frac{1}{2}$,1] | D. | [-1,$\frac{7}{3}$] |
分析 对x分x<$\frac{1}{2}$,$\frac{1}{2}$≤x≤1与x>1范围的讨论,去掉原不等式左端的绝对值符号,从而易解不等式|x-1|+|2x-1|≤5的解集.
解答 解:当x<$\frac{1}{2}$时,|x-1|+|2x-1|≤5?-x+1-2x+1≤5,
解得:-1≤x<$\frac{1}{2}$;
当$\frac{1}{2}$≤x≤1时,|x-1|+|2x-1|≤5?-x+1+2x-1≤5恒成立,
∴$\frac{1}{2}$≤x≤1;
当x>1时,|x-1|+|2x-1|≤5?x-1+2x-1=3x-2≤5,
解得:1<x≤$\frac{7}{3}$.
综上所述,不等式|x-1|+|2x-1|≤5的解集为[-1,$\frac{7}{3}$].
故选:D.
点评 本题考查绝对值不等式的解法,去掉绝对值符号是关键,考查分类讨论思想与运算求解能力,属于中档题.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 3π | B. | 6 | C. | 12 | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,将平面直角坐标系中的格点(横、纵坐标均为整点的点)按如下规则标上数字标签:点(0,0)处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,点(-1,1)处标6,点(0,1)处标7,依此类推,则标签20172的格点坐标 为(1009,1008).
如图,将平面直角坐标系中的格点(横、纵坐标均为整点的点)按如下规则标上数字标签:点(0,0)处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,点(-1,1)处标6,点(0,1)处标7,依此类推,则标签20172的格点坐标 为(1009,1008).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
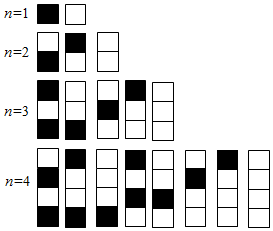 给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如图所示,由此推断,当n=6时,至少有两个黑色正方形相邻的着色方案共有( )种.
给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如图所示,由此推断,当n=6时,至少有两个黑色正方形相邻的着色方案共有( )种.| A. | 21 | B. | 32 | C. | 43 | D. | 54 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36种 | B. | 120种 | C. | 144种 | D. | 180种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com