
分析 (1)根据|$\overrightarrow{α}$|=|$\overrightarrow{b}$|列出方程解出α;
(2)求出$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的坐标,得出|$\overrightarrow{c}$|的坐标,求出$\frac{|x|}{|\overrightarrow{c}|}$的平方,根据二次函数的性质求出$\frac{|x|}{|\overrightarrow{c}|}$的最大值.
解答 解:(I)∵|$\overrightarrow{α}$|=|$\overrightarrow{b}$|,∴2sin2α=cos2α+sin2α=1,
∴sin2α=$\frac{1}{2}$,∵α∈[$\frac{π}{2}$,π],
∴α=$\frac{3π}{4}$.
(II)$\overrightarrow{a}$=(cos$\frac{π}{4}$,sin$\frac{π}{4}$),$\overrightarrow{b}$=(cos$\frac{3π}{4}$,sin$\frac{3π}{4}$).
∴$\overrightarrow{{e}_{1}}$=(0,1),$\overrightarrow{{e}_{2}}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
∴$\overrightarrow{c}=(\frac{y}{2},x+\frac{\sqrt{3}y}{2})$.
∴|$\overrightarrow{c}$|=$\sqrt{(\frac{y}{2})^{2}+(x+\frac{\sqrt{3}y}{2})^{2}}$=$\sqrt{{x}^{2}+{y}^{2}+\sqrt{3}xy}$.
∴$\frac{|x{|}^{2}}{|\overrightarrow{c}{|}^{2}}$=$\frac{{x}^{2}}{{x}^{2}+{y}^{2}+\sqrt{3}xy}$=$\frac{1}{1+(\frac{y}{x})^{2}+\frac{\sqrt{3}y}{x}}$=$\frac{1}{[(\frac{y}{x})+\frac{\sqrt{3}}{2}]^{2}+\frac{1}{4}}$.
∴当$\frac{y}{x}=-\frac{\sqrt{3}}{2}$时,$\frac{|x{|}^{2}}{|\overrightarrow{c}{|}^{2}}$取得最大值4.
∴$\frac{|x|}{|\overrightarrow{c}|}$的最大值是2.
点评 本题考查了平面向量的数量积运算,向量的坐标运算,二次函数的最值,属于中档题.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-y+1=0 | B. | x+y+1=0 | C. | x+y-7=0 | D. | x-y-7=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
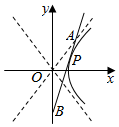 已知双曲线C的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),离心率e=$\frac{\sqrt{13}}{2}$.
已知双曲线C的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),离心率e=$\frac{\sqrt{13}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com