练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．在△ABC中，4sinA=5sinB，cos（A-B）=$\frac{31}{32}$，则$\frac{a-b}{a+b}$=$\frac{1}{9}$，cosC=$\frac{1}{8}$．

    分析 利用正弦定理求得a，b，构造三角形，利用余弦定理求得BD的长，再求CD和AD的长，在等腰三角形中求cosC．

    解答 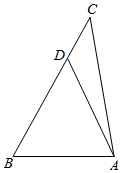解：由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$，即asinB=bsinA由已知可得a=5k，b=4k
    则$\frac{a-b}{a+b}$=$\frac{1}{9}$，
    ∵a＞b，∴A＞B．在BC上取D，使得BD=AD，连接AD，
    设BD=x，则AD=x，DC=5-x．
    在△ADC中，注意cos∠DAC=cos（A-B）=$\frac{31}{32}$，
    由余弦定理得：（5-x）2=x2+42-2x×4×$\frac{31}{32}$
    即：25-10x=16-$\frac{31}{4}$x，
    解得：x=4．
    ∴在△ADC中，AD=AC=4，CD=1，
    ∴cosC=$\frac{\frac{1}{2}CD}{AD}$=$\frac{1}{8}$
    故答案为：$\frac{1}{9}$，$\frac{1}{8}$

    点评 本题主要考察正弦余弦定理，构造三角形，求余弦值，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    16．已知函数y=2sin（2x+φ）（|φ|＜$\frac{π}{2}$）图象经过点（0，$\sqrt{3}$），则该函数图象的一条对称轴方程为（　　）
    A．x=$\frac{π}{6}$B．x=-$\frac{π}{12}$C．x=$\frac{π}{12}$D．x=-$\frac{π}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为$\frac{2π}{3}$，|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=3，则|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{7}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知P1，P2，…，Pn是曲线C：y=$\frac{1}{x}$（x＞0）上一系列点，且满足以下条件，过P1作直线l：y=1的垂线．垂足为A1，作线段P1A1的中垂线交曲线C于P2，再过P2作直线l的垂线，垂足为A2，作线段P2A2的中垂线交曲线C于P3，依此类推，设Pn（an，$\frac{1}{{a}_{n}}$），n=1，2，3…，且a1=$\frac{2}{3}$．
    （1）求{an}的通项公式；
    （2）求证：an≥-（1+$\frac{1}{{2}^{n}}-\frac{1}{x}$）x2+x对任意x∈R恒成立；
    （3）记数列{an}的前n项和为Sn，求证：Sn＞$\frac{{n}^{2}}{n+1}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．设集合A={1，2，4，5，6}，B={4，5，6，7}，求满足S⊆A．且S∩B≠∅的集合的个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．求符合下列条件的圆的方程：
    （1）圆心在点（0，2）且与直线x-2y+1=0相切；
    （2）圆心在x轴上，且过点（3，$\sqrt{3}$）、（0，0）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．设向量$\overrightarrow{α}$=（sinα，sinα）．$\overrightarrow{b}$=（cosα，sinα），α∈[$\frac{π}{2}$，π]且|$\overrightarrow{α}$|=|$\overrightarrow{b}$|．
    （I）求α的值；
    （II）将$\overrightarrow{b}$顺时针方向旋转$\frac{π}{4}$得到$\overrightarrow{{e}_{1}}$，将$\overrightarrow{α}$逆时针方向旋转$\frac{π}{12}$得到$\overrightarrow{{e}_{2}}$，非零向量$\overrightarrow{c}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$，求$\frac{|x|}{|\overrightarrow{c}|}$的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．根据下列条件，求角α的指定的三角函数值：
    （1）已知sin$α=-\frac{\sqrt{3}}{2}$，且α是第三象限角，求cosα和tanα；
    （2）已知tanα=-3，且α是第二象限角，求sinα和cosα；
    （3）已知cos$α=\frac{12}{13}$，且α是第四象限角，求sinα和tanα；
    （4）已知sin$α=-\frac{1}{2}$，α∈R，求cosα和tanα．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知全集U={1，2，3，4，5}，集合A=（1，2，5}，∁UB=（1，3，5}，则A∩B=（　　）
    A．{2}B．{5}C．{1，2，4，5}D．{3，4，5}

    查看答案和解析>>

    同步练习册答案