
分析 利用辅助角公式,易将其化为正弦型h或余弦型函数的形式.
解答 解:(1)5sinα-12cosα=13($\frac{5}{13}$sinα-$\frac{12}{13}$cosα)=13sin(α+φ),其中tanφ=$\frac{12}{5}$,
(2)$\frac{\sqrt{2}}{2}$cosα-$\frac{\sqrt{6}}{2}$sinα=$\sqrt{2}$($\frac{1}{2}$cosα-$\frac{\sqrt{3}}{2}$sinα)=$\sqrt{2}$cos(α+$\frac{π}{3}$),
(3)-$\frac{\sqrt{3}}{3}$sinα-cosα=-$\frac{2\sqrt{3}}{3}$($\frac{1}{2}$sinα+$\frac{\sqrt{3}}{2}$cosα)=-$\frac{2\sqrt{3}}{3}$sin(α+$\frac{π}{3}$).
点评 在三角函数中,我们常用辅助角公式asinα+bcosα=$\sqrt{{a}^{2}+{b}^{2}}$sin(α+φ),将三角函数的表达式化为正弦型函数的形式


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
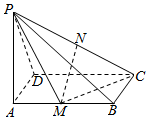 如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°.
如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
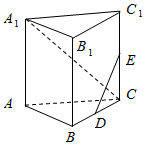 已知三棱柱ABC-A1B1C1,侧棱AA1垂直于底面ABC,∠$ABC=\frac{π}{2}$,AB=BC=AA1=4,D为BC的中点.
已知三棱柱ABC-A1B1C1,侧棱AA1垂直于底面ABC,∠$ABC=\frac{π}{2}$,AB=BC=AA1=4,D为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com