
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若函数![]() 在
在![]() 上至少有一个零点,求
上至少有一个零点,求![]() 的取值范围;
的取值范围;
(Ⅱ)若函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) ![]() 或
或![]() .
.
【解析】
试题(Ⅰ)根据方程的根与函数的零点的关系,将问题转化为函数对应的方程有至少一个根,那么由判别式与根的个数的关系可知,只要判别式大于或等于0即可,列不等式求解;(Ⅱ)先求出二次函数的对称轴,看看所给的闭区间与对称轴的关系,分![]() 和
和![]() 两种情况进行讨论:当
两种情况进行讨论:当![]() 时,左半区间在对称轴的左边,最大值是
时,左半区间在对称轴的左边,最大值是![]() ;当
;当![]() 时,右半区间在对称轴的右边,最大值是
时,右半区间在对称轴的右边,最大值是![]() .然后结合最大值是3来求解.
.然后结合最大值是3来求解.
试题解析:(Ⅰ)依题意,函数![]() 在
在![]() 上至少有一个零点
上至少有一个零点
即方程![]() 至少有一个实数根. 2分
至少有一个实数根. 2分
所以![]() ,
,
解得![]() . 5分
. 5分
(Ⅱ)函数![]() 图象的对称轴方程是
图象的对称轴方程是![]() .
.
①当![]() ,即
,即![]() 时,
时,![]() .
.
解得![]() 或
或![]() .又
.又![]() ,
,
所以![]() . 9分
. 9分
② 当![]() ,即
,即![]() 时,
时,
解得![]() .又
.又![]() ,
,
所以![]() . 13分
. 13分
综上,![]() 或
或![]() . 14分
. 14分


 每课必练系列答案
每课必练系列答案科目:高中数学 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,已知
,已知![]() ,
,![]() ,
,![]() .
.
(1)证明:![]() 为等比数列,求出
为等比数列,求出![]() 的通项公式;
的通项公式;
(2)若![]() ,求
,求![]() 的前n项和
的前n项和![]() ,并判断是否存在正整数n使得
,并判断是否存在正整数n使得![]() 成立?若存在求出所有n值;若不存在说明理由.
成立?若存在求出所有n值;若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论正确的是( )
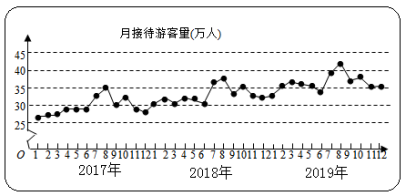
A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位数为30
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() .
.
(1)当![]() 时,判断曲线
时,判断曲线![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(2)当曲线![]() 上有且只有一点到曲线
上有且只有一点到曲线![]() 的距离等于
的距离等于![]() 时,求曲线
时,求曲线![]() 上到曲线
上到曲线![]() 距离为
距离为![]() 的点的坐标.
的点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() .现沿对角线
.现沿对角线![]() 将
将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() .点
.点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() 、
、![]() 、
、![]() 、
、![]() 四点共面.
四点共面.

(1)求证:![]() ;
;
(2)若平面![]() 平面
平面![]() ,平面
,平面![]() 与平面
与平面![]() 夹角为
夹角为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,以
的中点,以![]() 为圆心,
为圆心, ![]() 为半径的圆交
为半径的圆交![]() 于
于![]() ,点
,点![]() 在弧
在弧![]() 上运动(如图).若
上运动(如图).若![]() ,其中
,其中![]() ,
, ![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】湖南省会城市长沙又称星城,是楚文明和湖湘文化的发源地,是国家首批历史文化名城.城内既有岳麓山、橘子洲等人文景观,又有岳麓书院、马王堆汉墓等名胜古迹,每年都有大量游客来长沙参观旅游.为合理配置旅游资源,管理部门对首次来岳麓山景区游览的游客进行了问卷调查,据统计,其中![]() 的人计划只游览岳麓山,另外
的人计划只游览岳麓山,另外![]() 的人计划既游览岳麓山又参观马王堆.每位游客若只游览岳麓山,则记1分;若既游览岳麓山又参观马王堆,则记2分.假设每位首次来岳麓山景区游览的游客计划是否参观马王堆相互独立,视频率为概率.
的人计划既游览岳麓山又参观马王堆.每位游客若只游览岳麓山,则记1分;若既游览岳麓山又参观马王堆,则记2分.假设每位首次来岳麓山景区游览的游客计划是否参观马王堆相互独立,视频率为概率.
(1)从游客中随机抽取3人,记这3人的合计得分为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)从游客中随机抽取![]() 人(
人(![]() ),记这
),记这![]() 人的合计得分恰为
人的合计得分恰为![]() 分的概率为
分的概率为![]() ,求
,求![]() ;
;
(3)从游客中随机抽取若干人,记这些人的合计得分恰为![]() 分的概率为
分的概率为![]() ,随着抽取人数的无限增加,
,随着抽取人数的无限增加,![]() 是否趋近于某个常数?若是,求出这个常数;若不是,说明理由.
是否趋近于某个常数?若是,求出这个常数;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() 为正三角形,平面
为正三角形,平面![]() 平面
平面![]() ,
,![]() 是线段
是线段![]() 的中点,
的中点,![]() 是线段
是线段![]() 上的动点.
上的动点.
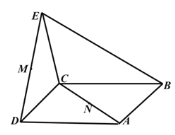
(1)探究![]() 四点共面时,
四点共面时,![]() 点位置,并证明;
点位置,并证明;
(2)当![]() 四点共面时,求
四点共面时,求![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com