
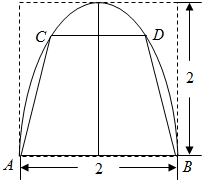
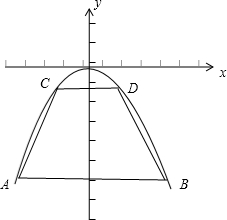
 ��ͼ����һ����������״�ĸְ壬�ƻ����˸ְ��и�ɵ�������ABCD����״��ʹ��A��B��C��D�������������ϣ���A��B���������ߵ���Գƣ���AB=2�������ߵĶ��㵽�ױߵľ�����2����CD=2t���������ΪS��
��ͼ����һ����������״�ĸְ壬�ƻ����˸ְ��и�ɵ�������ABCD����״��ʹ��A��B��C��D�������������ϣ���A��B���������ߵ���Գƣ���AB=2�������ߵĶ��㵽�ױߵľ�����2����CD=2t���������ΪS��| 1 |
| 3 |
| 64 |
| 27 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
|
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 64 |
| 27 |


 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��֪������R���溯��f��x�����㵱x��0ʱ��f��x��=|2x-2|��
��֪������R���溯��f��x�����㵱x��0ʱ��f��x��=|2x-2|���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 �������̲������Դ�;۾ӵأ����ˡ���ҵ�ķ�Դ�غ��̳�����Ľ����أ�����ʼ��������������������ǻ���֮������2006��11��10��������ٰ�����ʻ����Ļ��ڣ�ij���ܼ��Ÿ�����Ҫ������ͼ��ʾһ���λ�̳ABCD������һ������ľ��λ�̳AMPN��Ҫ��B����AM�ϣ�D����AN�ϣ��ҶԽ���MN��C�㣬��֪AB=3�ף�AD=2�ף�
�������̲������Դ�;۾ӵأ����ˡ���ҵ�ķ�Դ�غ��̳�����Ľ����أ�����ʼ��������������������ǻ���֮������2006��11��10��������ٰ�����ʻ����Ļ��ڣ�ij���ܼ��Ÿ�����Ҫ������ͼ��ʾһ���λ�̳ABCD������һ������ľ��λ�̳AMPN��Ҫ��B����AM�ϣ�D����AN�ϣ��ҶԽ���MN��C�㣬��֪AB=3�ף�AD=2�ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 2 |
| x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| �� |
| 3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com