
分析 (1)化简an+1=$\frac{{n}^{2}{a}_{n}}{{n}^{2}+1}$(n∈N+)后即可证明an+1<an;
(2)先验证n=1时成立,当n≥2时利用分离常数法化简后,由放缩法和裂项相消法证明不等式成立;
(3)由放缩法化简$\frac{{a}_{n+1}}{{a}_{n}}$后,列出不等式进行归纳、化简证明不等式成立.
解答 证明:(1)由an+1=$\frac{{n}^{2}{a}_{n}}{{n}^{2}+1}$(n∈N+)得,$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{{n}^{2}}{{n}^{2}+1}$<1,
∴an+1<an;
(2)当n=1时,$\frac{{a}_{1}}{{a}_{2}}=2$成立,
当n≥2时,∵$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{{n}^{2}}{{n}^{2}+1}$,则$\frac{{a}_{n}}{{a}_{n+1}}=\frac{{n}^{2}+1}{{n}^{2}}$=1+$\frac{1}{{n}^{2}}$,
∴$\frac{{a}_{1}}{{a}_{2}}+\frac{{a}_{2}}{{a}_{3}}+…+\frac{{a}_{n}}{{a}_{n+1}}$=n+$\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}+…+\frac{1}{{n}^{2}}$
≤n+1+$\frac{1}{1•2}+\frac{1}{2•3}+…+\frac{1}{(n-1)n}$
=n+1+(1-$\frac{1}{2}$)+($\frac{1}{2}-\frac{1}{3}$)+…+($\frac{1}{n-1}-\frac{1}{n}$)=n+2-$\frac{1}{n}$,
∴$\frac{{a}_{1}}{{a}_{2}}+\frac{{a}_{2}}{{a}_{3}}+…+\frac{{a}_{n}}{{a}_{n+1}}≤n+2-\frac{1}{n}$;
(3)由(1)得,$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{{n}^{2}}{{n}^{2}+1}$>$\frac{{n}^{2}-1}{{n}^{2}}$=$\frac{n-1}{n}•\frac{n+1}{n}$,
则an+1>an•$\frac{n-1}{n}•\frac{n+1}{n}$,
由a1=1得,a2=$\frac{1}{2}$,则n=1、2都成立,
当n≥3时,a3>a2•$\frac{1}{2}•\frac{3}{2}$,a4>a3•$\frac{2}{3}•\frac{4}{3}$>a2•$\frac{1}{2}•\frac{3}{2}$•$\frac{2}{3}•\frac{4}{3}$,…
∴an>a2•$\frac{1}{2}•\frac{3}{2}$•$\frac{2}{3}•\frac{4}{3}$…$\frac{n-2}{n-1}•$$\frac{n}{n-1}$=$\frac{n}{4(n-1)}$$>\frac{1}{4}$,
综上可得,an$>\frac{1}{4}$对一切n∈N+都成立.
点评 本题考查数列递推式的化简和应用,以及裂项相消法求和,利用放缩法、归纳推理证明不等式等,考查化简、变形能力,分析问题、解决问题的能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1+$\sqrt{6}$ | B. | -1+2$\sqrt{6}$ | C. | -1+$\sqrt{5}$ | D. | -1+2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1<a<2 | B. | a>2或a<-1 | C. | a≥2或a≤-1 | D. | a>1或a<-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(0)<f(-$\frac{1}{3}$)<f($\frac{2}{5}$) | B. | f(-$\frac{1}{3}$)<f(0)<f($\frac{2}{5}$) | C. | f($\frac{2}{5}$)<f(-$\frac{1}{3}$)<f(0) | D. | f(0)<f($\frac{2}{5}$)<f(-$\frac{1}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
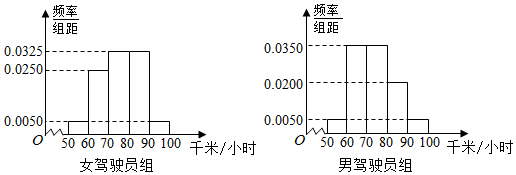
| 危险驾驶 | 非危险驾驶 | 合计 | |
| 男驾驶员 | 15 | 45 | 60 |
| 女驾驶员 | 15 | 25 | 40 |
| 合计 | 30 | 70 | 100 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 正方体ABCD-A1B1C1D1中,点M是CD的中点.
正方体ABCD-A1B1C1D1中,点M是CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com